Wie weit ist der Horizont entfernt?
Wollten Sie schon immer wissen, wie weit der Horizont entfernt ist, wenn Sie aufs Meer hinausblicken? Oder wie hoch Sie ins Weltall reisen müssten, um die gesamte Erdkugel erblicken zu können? Hier kommen die Antworten.

Wie weit mag der Horizont auf diesem Bild entfernt sein?
Foto: Panthermedia.net/Yuri Arcurs
Pünktlich zum Ferienstart machen sich jedes Jahr unzählige Menschen auf den Weg zum Meer. Beim Blick auf die unendlichen Weiten des Wassers haben sich bestimmt viele bereits einmal gefragt, wie weit diese „Unendlichkeit“ reichen mag, also wie weit der Horizont entfernt ist. Ingenieure mögen das recht einfach ausrechnen können, wir möchten es uns in diesem Beitrag dennoch einmal etwas genauer anschauen. Außerdem verraten wir Ihnen, wie hoch Sie ins Weltall müssten, um die gesamte Erdkugel auf einmal sehen zu können.
Entfernung hängt von der Höhe des Betrachters ab
Es gibt keine festgelegte Obergrenze, da der Horizont vom Betrachter aus gesehen umso weiter entfernt ist, je höher sein Standpunkt ist. Die gekrümmte Oberfläche der Erde ermöglicht es uns, mit jedem Schritt auf einem Turm oder einer Leiter ein wenig weiter zu sehen.
Um dies besser zu verstehen, können wir uns vorstellen, einen großen Kreisbogen auf ein Blatt Papier zu zeichnen, der die Erdoberfläche darstellt. Senkrecht zum Kreisbogen zeichnen wir einen kurzen Strich, der den Betrachter repräsentiert. Vom oberen Ende des Strichs ziehen wir dann eine Linie, die den Kreisbogen gerade berührt. Dieser Berührungspunkt wird als Horizont bezeichnet. Es wird deutlich, dass je länger der Strich ist, desto länger wird auch die Verbindungslinie zum Kreisbogen.
Bei Berechnung des Horizonts hilft Satz des Pythagoras
Die Größenverhältnisse auf dem Papier sind natürlich nicht realistisch, aber durch das Aufmalen wird deutlich, dass man die Entfernung zum Horizont letztendlich mit dem Satz des Pythagoras berechnen kann. Dazu benötigt man die Augenhöhe des Betrachters sowie den mittleren Radius der Erde, der etwa 6.371 km beträgt. Zur Erinnerung, er lautet a² + b² = c². Die Seitenlänge a des rechtwinkligen Dreiecks entspricht dem Erdradius, den Wert b wollen wir berechnen, denn er entspricht dem Horizont. Der Wert c wiederum ist die Summe aus Erdradius plus Höhe des Betrachters über der Erdoberfläche.
Ein Mensch mit einer Größe von 1,80 Meter kann demnach 5 Kilometer weit blicken, setzt er sich in den Sand und ist nur noch 1 Meter über der Erde, sinkt die Blickweite auf 3,57 Kilometer. Steigen wir im Teneriffa-Urlaub auf den Pico del Teide, ist der Horizont fast 214 Kilometer entfernt. Der höchste Berg Spaniens ragt 3715 Meter über den Meeresspiegel hinaus. Bleiben wir beim Urlaub: Flugzeuge fliegen meist in einer Höhe von rund 10 Kilometern, schauen Sie dann aus dem Fenster, ist der Horizont fast 360 Kilometer entfernt.
Das sind alles nur Spielereien, doch es gibt auch praktische und nützliche Anwendungen, für die es wichtig ist, die Entfernung zum Horizont zu kennen. Zum Beispiel in der Schifffahrt und hier bei Leuchttürmen, die der Orientierung dienen. Wie weit mögen die wohl strahlen? Nehmen wir den Leuchtturm von Campen auf Sylt. Er ist mit rund 65 Metern der höchste Leuchtturm Deutschlands. Sein Leuchtfeuer ist in einer Höhe von 62 Metern und kann nach Berechnung mit dem Pythagoras noch in einer Entfernung von 28 Kilometern wahrgenommen werden (nn Wahrheit sind es noch mehr Kilometer, da das Licht auch nach oben abstrahlt).
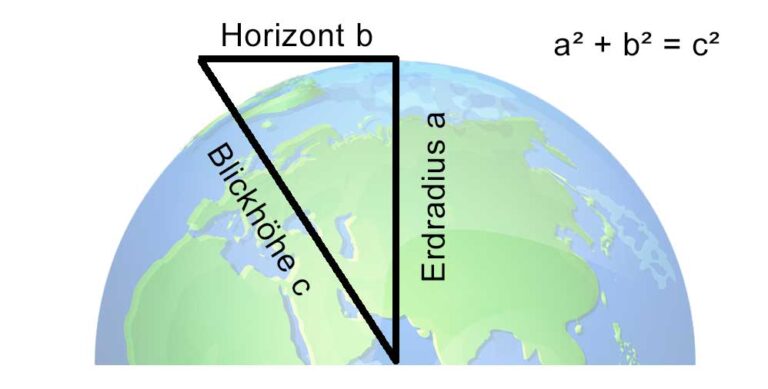
Mit Hilfe des Pythagoras lässt sich der Horizont recht leicht berechnen.
Foto: ingenieur.de (Grafik Erdkugel: Panthermedia.net/ClassyCatStudio)
Wo liegen die Grenzen der Berechnung?
Ein Betrachter kann beliebig weit von der Erde entfernt sein, und entsprechend weit wäre dann auch der Horizont entfernt. Daher wird diese Berechnung irgendwann sinnlos. Ein interessanter Ansatz wäre beispielsweise die Frage: Wie weit ist der Horizont für einen Betrachter auf dem Mond? Auf dem Mond hat man auch einen Horizont, der den sichtbaren Rand der Erde markiert. Logischerweise wäre dieser Horizont ungefähr so weit entfernt wie der Mond selbst, also etwa 400.000 Kilometer. Dennoch wird diese Entfernung hauptsächlich durch den Abstand zwischen dem Betrachter und der Erdoberfläche bestimmt. Die Berechnungsmethode bleibt jedoch im Wesentlichen dieselbe.
Wenn man die Frage etwas anders formuliert, nämlich nicht „Wie weit ist der Horizont vom Betrachter entfernt?“, sondern „Welche Entfernung auf der Erdoberfläche kann maximal überblickt werden?“, wird es klar: Auch vom Mond aus kann man nur die Hälfte der Erde sehen. Da der Erdumfang etwa 40.000 Kilometer beträgt, entspricht die Hälfte davon 20.000 Kilometern. Das ist die Entfernung von einem Ende der Erde zum anderen. Das führt zu einer weiteren Fragestellung, die wir im nächsten Abschnitt angehen möchten.
Wie hoch über der Erde muss man sein, um die ganze Erdkugel zu sehen?
Der deutsche Astronaut Thomas Reiter sagte in einem Interview mit dem Onlinemagazin National Geographic aus dem Jahr 2018: „Die Erde als komplette Kugel habe ich bei meinen beiden Ausflügen ins All leider nicht gesehen. Die Raumstationen Mir und ISS, auf denen ich gelebt und gearbeitet habe, sind zwischen 350 und 400 Kilometer von der Erde entfernt. Man erkennt die Krümmung des Erdballs und überblickt ganze Kontinente, wie zum Beispiel Europa. Das ist überwältigend!“
In einer Höhe von 350 Kilometern über der Erde ist der Horizont rund 2.140 Kilometer entfernt, in einer Höhe von 400 Kilometern sind es fast 2.300 Kilometer. Das reicht in der Tat noch nicht, die ganze Erdkugel auf einmal zu sehen. Dazu muss man noch etwas höher ins Weltall gehen. Doch wie hoch genau? Mit dem Satz des Pythagoras lässt sich auch das berechnen. Zusätzlich benötigen wir den Erdumfang. Dieser beträgt am Äquator rund 40.000 Kilometer, wie bereits erwähnt.
Da wir nur die eine Hälfte der Erde sehen können, ist der Horizont maximal 10.000 Kilometer entfernt. Dies entspricht einem Viertel des Erdumfangs, da wir immer in eine Richtung auf den Horizont blicken. Wenn wir diesen Wert zusammen mit dem Erdradius betrachten und wieder Pythagoras bemühen, können wir die erforderliche Blickhöhe berechnen. Diese beträgt etwa 5.500 Kilometer. Ab dieser Höhe haben Astronauten somit das Privileg, die Erde in ihrer vollen Pracht bewundern zu können.
Ein Beitrag von: