Strategie oder Zufall: Die Mathematik hinter den Lottozahlen
Ist Lotto reiner Zufall oder berechenbar? Ein Blick auf Wahrscheinlichkeiten, Strategien und mathematische Mythen rund um 6 aus 49.

Sechs aus 49 erklärt: Wie klein die Chancen wirklich sind und warum clevere Tipps den Zufall nicht schlagen.
Foto: Smarterpix / Regormark
Der Autor dieser Zeilen hatte in den vergangenen Tagen zweimal vier Richtige beim Lotto 6 aus 49, einmal sogar mit Superzahl. Das sicherte ihm zumindest die Urlaubsspesen, denn er befand sich gerade auf Fuerteventura. Das ist allerdings nichts im Vergleich zu drei Glückspilzen aus Bayern, auf die Millionengewinne warten. Ihr Pech: Bisher haben sie sich noch nicht gemeldet, sodass der Gewinn möglicherweise verfällt. Das nur am Rande. Wir wollen uns hier mit der Mathematik hinter den Lottozahlen beschäftigen. Ist alles nur Zufall oder hilft eine Strategie beim Lottospielen?
Inhaltsverzeichnis
- Erst die harte Grundlage: Was „6 aus 49“ mathematisch ist
- „Heiß“ und „kalt“: Warum die Trommel kein Gedächtnis hat
- Was bedeutet „1 zu 140.000.000“ konkret?
- „Aber ich hatte doch vier Richtige“ – ja, und das ist mathematisch plausibel
- Der wichtigste Begriff, den kaum jemand nutzt: Erwartungswert
- Mit welcher Strategie klappt es mit dem Lottogewinn?
- Lässt sich Lotto austricksen?
- Graphen, Ebenen und Zahlentripel
- Der Kern der Sache
Erst die harte Grundlage: Was „6 aus 49“ mathematisch ist
Lotto 6 aus 49 ist ein Standardfall der Kombinatorik und Stochastik. Sie ziehen ohne Zurücklegen aus 49 Kugeln genau 6. Die Reihenfolge ist egal. Jede 6er-Kombination ist gleich wahrscheinlich.
Die zentrale Größe heißt Binomialkoeffizient:
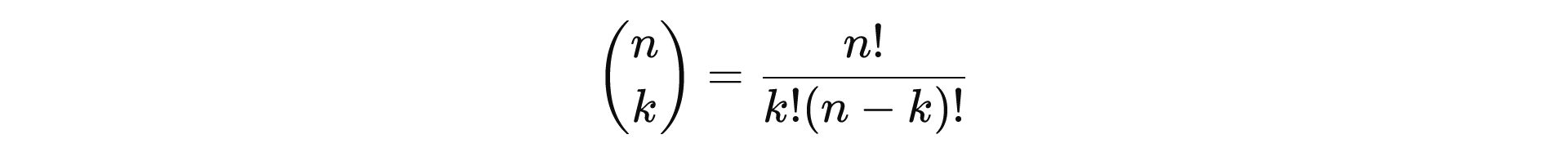
Für Lotto 6 aus 49 sieht das so aus:
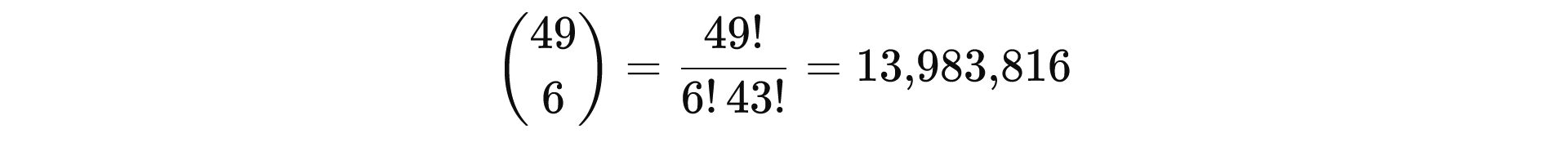
Das ist die Anzahl aller möglichen 6er-Kombinationen. Genau eine davon ist der Treffer für „6 Richtige“.
Damit gilt:
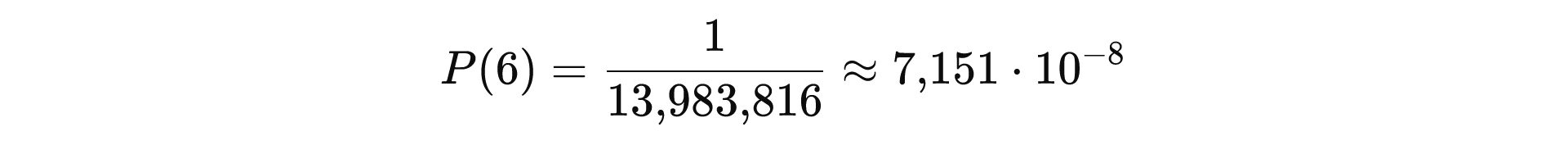
Als „1 zu …“:
- 6 Richtige (ohne Superzahl): ca. 1 : 13.983.816 (oft gerundet zu ~1:14 Mio.)
Die Superzahl ist eine zusätzliche Ziffer von 0 bis 9. Wenn Sie sie als unabhängig behandeln (praktisch: 1 von 10 passt), dann:
- 6 Richtige + Superzahl: ca. 1 : 139.838.160
Diese Zahlen folgen direkt aus der Kombinatorik, einem Teilgebiet der Mathematik, das sich mit der Anzahl möglicher Anordnungen beschäftigt. Wer Lotto spielt, nimmt also bewusst an einem extrem ungünstigen Zufallsexperiment teil.
„Heiß“ und „kalt“: Warum die Trommel kein Gedächtnis hat
Viele Spielende interpretieren Ziehungen wie Wetter. Zahlen seien „fällig“. Oder „zu oft gekommen“. Mathematisch ist das die Spieler-Fehlschlussfalle (gambler’s fallacy).
Jede Ziehung ist (idealisiert) ein unabhängiges Zufallsexperiment. Vorherige Ziehungen ändern die Wahrscheinlichkeiten nicht. Das Statement dazu ist klar: „Den einen Tipp an sich gibt es nicht”, stellt der Meißener Mathematiker Norbert Herrmann klar. Und noch direkter: Die Maschine hat keine Moral und keine Erinnerung. Sie zieht nicht, weil „jetzt mal die 37 dran ist“.
Was bedeutet „1 zu 140.000.000“ konkret?
Weiter oben haben wir die Wahrscheinlichkeit für den Gewinn des Jackpots berechnet. Sie liegt bei etwa 1 zu 140.000.000. Das ist „6 Richtige + Superzahl“. Rechnen Sie das in Erwartungszeiten um, wird es greifbarer:
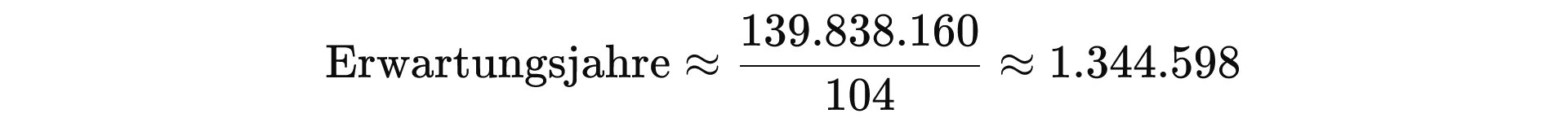
Interpretation:
Im statistischen Mittel müssten Sie rund 1,34 Millionen Jahre lang jede Woche spielen, um einmal den Jackpot zu treffen.
Zur Klarstellung: Das ist ein Erwartungswert eines geometrischen Prozesses, keine Vorhersage. Einzelne Gewinne können früher auftreten, die große Mehrheit tritt nie ein.
„Aber ich hatte doch vier Richtige“ – ja, und das ist mathematisch plausibel
Ich hatte eingangs geschrieben, dass ich innerhalb weninger Tage gleich zweimal Vier Richtige hatte. Mathematisch betrachtet ist das sicherlich selten, aber nicht astronomisch. Grob: 1:1.147 (ohne Superzahl) oder 1:10.324 (mit Superzahl) – je nachdem, wie man die Klasse definiert.
Das erklärt, warum in großen Populationen regelmäßig Leute vier oder fünf Richtige haben. Viele spielen, also treten auch seltene Ereignisse sichtbar auf. Der Denkfehler entsteht, wenn Menschen aus einem persönlichen Treffer schließen: „Da ist ein Muster.“ Nein. Sie haben einen Treffer aus einem großen Zufallsraum erlebt.
Der wichtigste Begriff, den kaum jemand nutzt: Erwartungswert
Die zentrale Frage lautet nicht „Kann ich gewinnen?“. Die lautet: Wie ist der Erwartungswert meines Einsatzes?
Ein Glücksspiel ist dann mathematisch „fair“, wenn der Erwartungswert E = 0 ist (Auszahlung im Mittel = Einsatz). Lotto ist es nicht. Der Erwartungswert ist negativ, weil Betreiberkosten, Steuern, Abgaben, Jackpot-Rollover und Ausschüttungsquoten wirken.
Formel:
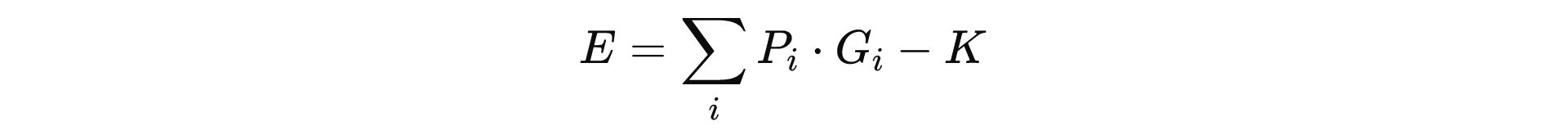
- Pi: Wahrscheinlichkeit für Gewinnklasse III
- Gi: Auszahlung in € in Klasse III
- K: Kosten pro Tipp
Ohne konkrete Auszahlungstabelle der jeweiligen Ziehung können Sie E nicht exakt numerisch ausrechnen. Aber die Struktur bleibt: Selbst perfekte Zufallstipps ändern Pi nicht. Strategie ist hier meist nur Kosmetik.
Mit welcher Strategie klappt es mit dem Lottogewinn?
Wir haben gelernt, dass sich die Wahrscheinlichkeit eines Lottogewinns mathematisch berechnen lässt. Doch gibt es Strategien, mit denen ein Gewinn zu 100 % sicher ist? Wir schauen uns drei Möglichkeiten an.
Strategie 1: „Viele Scheine kaufen“ – Trivial korrekt, praktisch teuer
Auf den ersten Blick wirkt es plausibel: Wer mehr Lottoscheine abgibt, erhöht seine Gewinnchance. Das stimmt. Jeder zusätzliche Tipp ist ein weiterer, unabhängiger Versuch. Damit wächst die Wahrscheinlichkeit, dass zumindest einer davon trifft.
Entscheidend ist jedoch, wie diese Chance wächst. Beim Lotto 6 aus 49 ist die Gewinnchance pro Tipp extrem klein. Mehrere Tipps addieren diese Chancen nahezu eins zu eins. Zehn Tipps bedeuten etwa die zehnfache Gewinnchance, hundert Tipps die hundertfache.
Das ist mathematisch unspektakulär. Sie betreten den Zufallsraum einfach öfter. Jeder Tipp deckt eine weitere von rund 14 Millionen möglichen Zahlenkombinationen ab. Mehr Tipps bedeuten nichts anderes als mehr abgedeckte Kombinationen.
Der Einsatz steigt dabei im gleichen Maß. Wer zehnmal so viele Tipps abgibt, zahlt zehnmal so viel. Die Gewinnchance pro eingesetztem Euro bleibt gleich. „Viele Scheine kaufen“ ist daher korrekt im Sinne der Wahrscheinlichkeitsrechnung, aber keine clevere Strategie – nur eine teure Wiederholung desselben Zufalls.
Strategie 2: „Systemschein“ – Sie ändern Varianz, nicht Physik
Systemspiele decken mehrere Kombinationen ab. Genau dafür sind sie da. Ihre Trefferwahrscheinlichkeit in unteren Klassen steigt. Aber: Ihre Kosten steigen auch.
Die Mathematik ist die gleiche wie oben, nur mit einer höheren Anzahl an abgegebenen Tipps. Das Ergebnis: öfter kleinere Gewinne, aber nicht „im Mittel profitabel“. Wenn Ihnen jemand verspricht, ein System mache das Spiel „gewinnbar“, dann ist das unseriös. Es kann Ihren Erlebniswert verbessern. Nicht die Grundökonomie.
Strategie 3: Wenn Mathematik kurzfristig funktioniert
Es gab Ausnahmen. Eine bekannte stammt vom Massachusetts Institute of Technology. Der Mathematiker James Harvey analysierte Anfang der 2000er Jahre eine US-Lotterie namens „Cash Winfall“. Dort wurde der Jackpot ab einer bestimmten Höhe nicht weiter angesammelt, sondern auf alle Gewinnenden verteilt.
Harvey erkannte eine mathematische Schwachstelle. In diesem Sonderfall stieg der erwartete Gewinn über den Einsatz. Gemeinsam mit Kommilitoninnen und Kommilitonen kaufte er Hunderttausende Lose. Das Team gewann mehrere hunderttausend Dollar.
Wichtig ist: Die Lotterie wurde danach geändert. Der Effekt verschwand. Die Strategie funktionierte nicht wegen Glück, sondern wegen einer fehlerhaften Spielregel. Sobald diese korrigiert war, war auch die Rendite weg.
Lässt sich Lotto austricksen?
Auch theoretisch lässt sich Lotto „austricksen“. Die britischen Mathematiker David Cushing und David Stewart berechneten 2023, dass man mit exakt 27 Lottoscheinen im britischen Lotto garantiert gewinnt – unabhängig von der Ziehung.
Der Haken: Der garantierte Gewinn liegt in den unteren Klassen. Der Einsatz übersteigt den Ertrag. Die beiden testeten ihre Methode selbst und verloren Geld. Ihr Fazit:
„Dieser unglückliche Vorfall belegt sowohl unser Ergebnis als auch den Grundsatz, dass man beim Glücksspiel immer damit rechnen sollte, Geld zu verlieren.“ Ihre Erfahrungen haben sie in dieser Forschungsarbeit niedergeschrieben.
Graphen, Ebenen und Zahlentripel
Warum ist das alles so kompliziert? Weil Lotto kombinatorisch extrem dicht ist. Mathematikerinnen und Mathematiker übersetzen Lotto-Probleme deshalb in Graphen. Jede mögliche Zahlenkombination wird zu einem Punkt. Punkte werden verbunden, wenn sie gemeinsame Zahlen enthalten.
Schon beim deutschen Lotto entsteht so ein Netzwerk mit knapp 14 Millionen Punkten und Milliarden Verbindungen. Gesucht sind sogenannte stabile Mengen: Kombinationen, die sich möglichst wenig überschneiden. Sie garantieren Treffer in unteren Gewinnklassen.
In kleinen Lotterien lässt sich das elegant lösen. Ein bekanntes Beispiel ist die sogenannte Fano-Ebene. Sie zeigt, wie man bei sieben Zahlen mit sieben Tipps garantiert mindestens zwei Richtige erzielt. Doch selbst dort bleibt der Erwartungswert negativ.
Der Kern der Sache
Lotto ist kein Rätsel, das man lösen kann. Es ist ein streng definiertes Zufallsexperiment. Mathematik kann erklären, wie unwahrscheinlich der Gewinn ist. Sie kann Sonderfälle identifizieren, wenn Spielregeln fehlerhaft sind. Sie kann Tipps geben, wie man Gewinne weniger oft teilen muss.
Was sie nicht kann: aus einem fairen Glücksspiel ein profitables System machen. Oder, nüchtern formuliert: Lotto ist Unterhaltung mit Preisetikett. Wer spielt, kauft Hoffnung. Nicht mehr, nicht weniger.
Ein Beitrag von:













