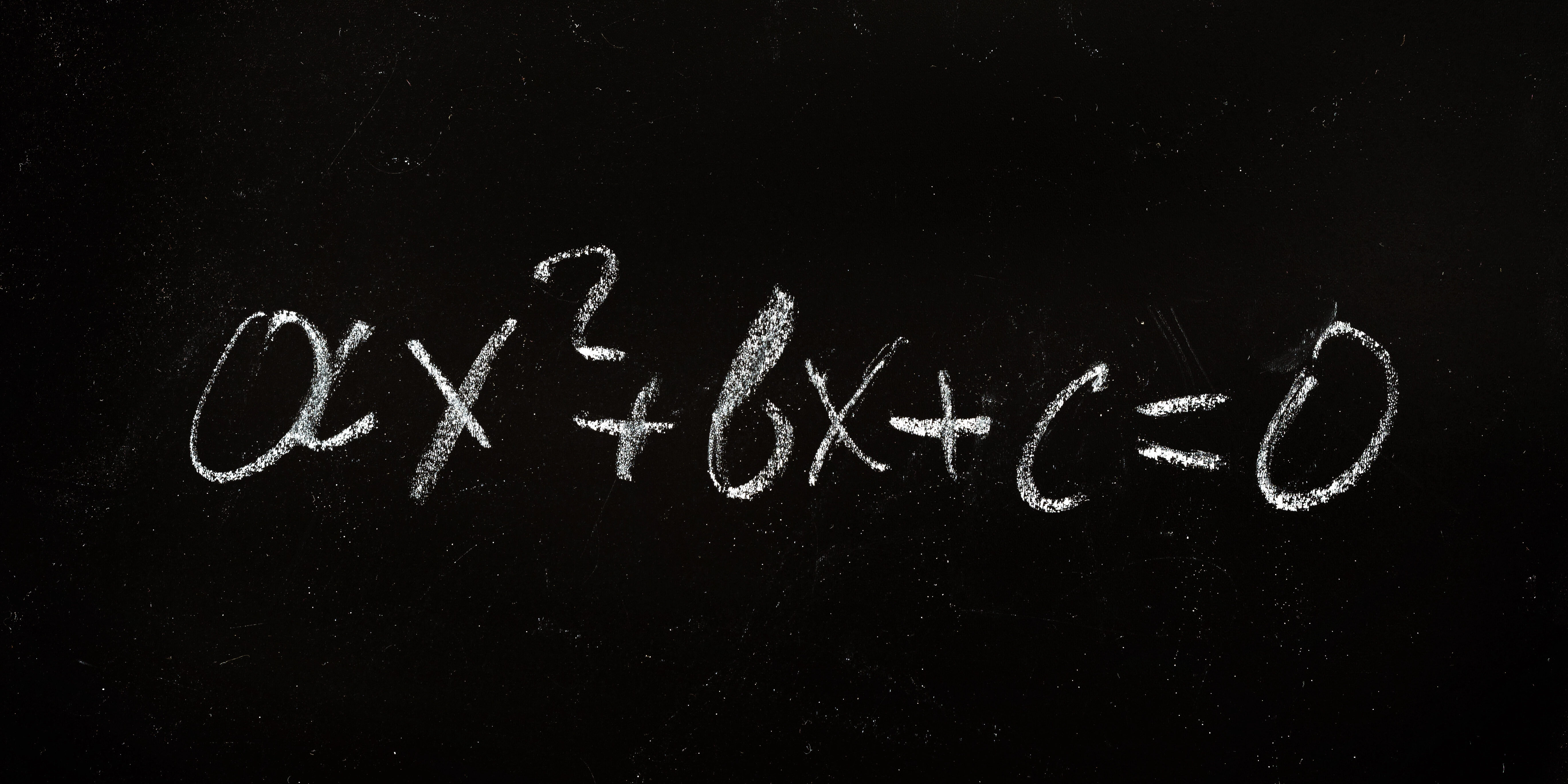Mischen für Fortgeschrittene oder alte Formel neu gedacht
Wie eine alte Formel neue Lösungen für technische Probleme liefert – von Materialverhalten bis Risikoabschätzung.

Die Borell-Brascamp-Lieb-Ungleichung beschreibt, wie sich Eigenschaften beim Mischen verändern – eine Formel mit weitreichender Bedeutung für Forschung und Technik.
Foto: Erika Fukuhara/OIST, using equations from Ishige et al., Math. Ann., 2025. Creative Commons Lizenz CC BY 4.0
Ein internationales Forschungsteam hat einen neuen Zugang zur Borell-Brascamp-Lieb-Ungleichung (BBL) gefunden. Statt wie bisher mit konvexer Analysis oder optimalem Transport zu arbeiten, stützt sich der neue Beweis auf Diffusionsprozesse und Wärmeleitung.
Dieser Ansatz eröffnet neue Perspektiven auf mathematische Beziehungen – und macht sie für Ingenieurinnen und Ingenieure in vielen Bereichen anwendbar. Die BBL hilft zu verstehen, wie sich Formen, Stoffe oder Wahrscheinlichkeiten beim Mischen verhalten. Besonders spannend: Anwendungen reichen von der medizinischen Bildverarbeitung über den Leichtbau bis zur Risikobewertung.
Inhaltsverzeichnis
Neue Wege zur perfekten Kombination
Was passiert, wenn zwei Dinge miteinander verschmelzen? Diese scheinbar einfache Frage stellt sich nicht nur in der Praxis, sondern auch in der Mathematik – und das mit großer Tiefe. Im Mittelpunkt steht dabei eine spezielle Ungleichung: die Borell-Brascamp-Lieb-Ungleichung (BBL). Sie beschreibt, wie sich Eigenschaften wie Dichte, Form oder Intensität verändern, wenn zwei Systeme kombiniert werden.
Ein Team vom Okinawa Institute of Science and Technology (OIST), der Universität Tokio und der Universität Florenz hat nun eine neue Herangehensweise vorgestellt. Statt wie bisher auf klassische Methoden zurückzugreifen, nutzten die Forschenden Diffusionsgleichungen – und zeigten damit, dass sich mathematische Zusammenhänge auch aus der Perspektive physikalischer Prozesse betrachten lassen.
Wie lässt sich eine Mischung mathematisch beschreiben?
„Mathematiker verwenden seit langem Ungleichungen, um Beziehungen zu beschreiben“, erklärt Prof. Qing Liu, der die Studie leitete. Die BBL-Ungleichung sei dabei besonders hilfreich, wenn es darum gehe, Veränderungen beim Mischen zweier Stoffe oder Systeme zu beschreiben. Ziel sei es gewesen, die andere Richtung zu untersuchen: Können sich aus physikalischen Modellen – konkret aus Diffusionsgleichungen – Rückschlüsse auf die mathematischen Strukturen ziehen lassen?
Dazu nutzten Liu und seine Kolleginnen und Kollegen sogenannte nichtlineare partielle Differentialgleichungen (PDEs). Solche Gleichungen sind zentral für die Beschreibung physikalischer Prozesse wie Wärmeleitung, Materialverteilung oder Ausbreitung chemischer Reaktionen.
Im konkreten Fall analysierten die Forschenden, wie sich Substanzen durch poröse Materialien bewegen. Das war jedoch nur der Ausgangspunkt: Ihr eigentliches Ziel war es, die mathematische Struktur der BBL-Ungleichung aus dieser Perspektive neu zu erfassen – und so auch deren Anwendung zu erweitern.
Was die Borell-Brascamp-Lieb-Ungleichung besonders macht
Die BBL ist nicht irgendeine Gleichung. Sie baut auf zwei etablierten Konzepten auf: der Brunn-Minkowski-Ungleichung und der Prékopa-Leindler-Ungleichung. Beide beschreiben, wie sich das Volumen oder andere Eigenschaften von Körpern oder Funktionen beim Kombinieren verändern.
Ein bildhaftes Beispiel liefert Prof. Liu selbst: „Stellen Sie sich vor, Sie möchten einen Film erstellen, in dem sich eine Form nahtlos in eine andere verwandelt – zum Beispiel einen Kreis in ein Quadrat. Damit dieser Übergang natürlich wirkt, müssen die Formen dazwischen ohne seltsame Verzerrungen wachsen oder schrumpfen.“
Solche Überlegungen sind keineswegs rein theoretisch. In der medizinischen Bildgebung etwa ist es wichtig, Veränderungen im Gewebe über die Zeit hinweg genau zu erfassen. Die mathematischen Grundlagen solcher Transformationen lassen sich mit der BBL nachvollziehen und modellieren.
Relevanz für Ingenieure
Die neue Sichtweise auf die BBL-Ungleichung eröffnet auch für Ingenieur*innen vielfältige Perspektiven. Denn die Anwendungen gehen weit über die Mathematik hinaus. Drei Beispiele:
- Baustoffe und Energie: Nichtlineare PDEs beschreiben, wie Wärme durch Festkörper fließt oder wie Stoffe sich in porösen Medien wie Beton bewegen. Für das Bauingenieurwesen oder die Verfahrenstechnik ist das zentral – etwa bei der Bewertung von Materialeigenschaften oder der Planung von Wärmespeichern.
- Bildverarbeitung und Simulation: In der optischen Messtechnik oder Medizintechnik geht es oft um die präzise Erkennung und Verfolgung von Formveränderungen – zum Beispiel bei der Überwachung von Tumoren oder der Analyse von Defekten. Mathematische Modelle wie die BBL helfen, diese Prozesse verständlich und effizient darzustellen.
- Risikomanagement und Optimierung: Auch im Systems Engineering oder der Regelungstechnik spielt Mathematik eine Rolle. Die BBL unterstützt hier beim Modellieren von Unsicherheiten, bei der Verteilung begrenzter Ressourcen oder bei der Bewertung von Risiken – etwa in der Prognose von Systemverhalten unter verschiedenen Szenarien.
Neue Beweise, neue Möglichkeiten
Warum sind mathematische Beweise wie dieser eigentlich so wichtig? Ganz einfach: Sie liefern das Fundament, um solche Gleichungen in der Praxis verlässlich anzuwenden. Bisher beruhte der Beweis der BBL auf Methoden aus der konvexen Geometrie oder dem optimalen Transport. Der nun gewählte Weg über Diffusionsprozesse eröffnet neue Einblicke – auch in die zugrunde liegende Struktur der Gleichung.
Die Forschenden betonen, dass ihr Ansatz nur ein Anfang sei. In Zukunft wollen sie sich nicht nur auf den euklidischen Raum konzentrieren – also eine Umgebung mit klaren Längen und Winkeln – sondern auch komplexere mathematische Räume untersuchen, in denen solche Strukturen nicht existieren. Das Ziel: Die Anwendungsmöglichkeiten der PDEs auf weitere mathematische Probleme ausweiten.
Ein Beitrag von: