Amplitudenmodulation – Wirkung auf den Menschen, Richtcharakteristik und Dopplereffekt
Zusammenfassung Ein Ansatz zur Bewertung der Wirkung der Amplitudenmodulation (AM) von Windenergieanlagen(WEA) bei Menschen wird ausgehend von Schallpegelmessungen bei Windparks und Einzelanlagen in der Praxis entwickelt. Aus Vorwissen der Literatur und eigenen Messungen werden Hörproben aus Messdaten erarbeitet und diese Stimuli von Probanden beurteilt. Die Ergebnisse der Hörversuche validieren die prognostizierte Wirkungsfunktion, sodass sie als eine operative Hilfe zur Entwicklung von Schallminderungsmaßnahmen dienen kann. Im zweiten Teil der Untersuchung wird auf die Richtungsabhängigkeit der AM, nicht zu verwechseln mit der Richtwirkung der WEA, eingegangen. Die Richtungsabhängigkeit der AM lässt sich im Rahmen eigener, simultaner Feldmessungen an Messpunkten in verschiedenen Richtungen zu einer WEA der 3 MW Klasse nachweisen. Die Richtungsabhängigkeit der AM und die Richtwirkung der WEA sind zumindest quer zu den WEA entgegengesetzt. Zusätzlich werden bei diesen Messungen Schmalbandanalysen der erhobenen Daten durchgeführt. Basis hierfür ist ein post processing der aufgenommenen Original Wav-Messdaten. Für die Schmalbandanalyse wird hier ein Analyse Tool verwendet, das eine Bandbreite der Bänder von 1/48 Oktave vorsieht. Die Auswertungen erfolgen im Bereich von 6 Hz bis 20 kHz. Die Auswertung liefert Sonogramme, aus denen in feiner Zeitauflösung das Geräuschemissionsverhalten der WEA zeitlich und frequenzabhängig aufgezeigt werden kann. Der Doppler-Effekt (Verstärkungsfaktor) ist hierbei ein wichtiger identifizierbarer Parameter der Geräuschcharakteristik. Durch ihn können übrigens Einzeltöne verbreitert werden. Schließlich erhält man hiermit ein eindeutiges Unterscheidungsmerkmal dieser Schallquellenart.

Die Amplitudenmodulation (AM) der Geräusche von Windenergieanlagen (WEA) ist ein aktuelles Thema der Umweltakustik und auch des Einsatzes von erneuerbaren Energien.
In unserer Arbeit [1] wurden verschiedene Praxisbeispiele des Auftretens von AM bei WEA vorgestellt, die im Prinzip nicht von den Ergebnissen anderer Autoren weltweit abweichen. Dazu wurde ein eigenes Verfahren zur Quantifizierung der Breite der Amplitudenmodulation vorgeschlagen. Das Verfahren verwendet die üblichen Messdaten LAF(t) bzw. LAeq in 100 ms – 125 ms- Takt, berechnet mit Hilfe der Wavelet-Transformation die dazugehörige Trendkorrektur in Zeitabschnitten von rd. 2 Minuten Dauer und ermöglicht die Angabe der Kenngrößen pAM5-m bzw. pAM1-m als Kenngröße zur Kennzeichnung der Breite der AM von Immissionspegeln aus WEA, sei es Einzelanlagen oder Windparks für z. B. Stundenintervalle.
Der Beitrag [1] schloss mit Bemerkungen zur subjektiven Einschätzung der AM und mit Hinweisen von anderen Autoren, wie eine Dosis-Wirkungs-Beziehung aussehen kann, die diese Wirkung angemessen beschreibt. In dieser Arbeit werden die Ergebnisse der weiteren Auswertungen zur Bestimmung der Wirkung der WEA-Geräusche auf den Menschen, unter dem besonderen Aspekt der AM mitgeteilt [2] und somit die ursprünglichen Untersuchungen nach [1] abgeschlossen.
Im zweiten Teil dieser Arbeit werden z. T. ergänzend zu Aussagen aus der Theorie und aus Messungen anderer Autoren, eigene Messungen im Rahmen der Arbeiten [3] und [4] an einer Einzel-WEA aus einem Windpark dargestellt. Es handelt sich dabei um – nach unserer Ansicht – fundamentale Darstellungen zum Verständnis der AM und der Geräuschcharakteristik der WEA als eine zugleich stationäre wie auch bewegte Schallquelle.
Dabei wird im Detail in [3] auf die Richtcharakteristik der AM einer WEA – nicht zu verwechseln mit der Richtcharakteristik der WEA im Sinne von [5], [6] – eingegangen. Zusätzlich wird unter Berücksichtigung der Theorie gemäß [7] (u. a.) die Amplitudenverstärkung durch den Doppler-Effekt in der Arbeit [4] näher untersucht.
Für die o. a. Arbeiten zur Ermittlung der Wirkung von WEA-Geräusche auf Menschen (vgl. [2]) wurden eigens die Wirkungsfunktion entwickelt sowie die (Hör-)Versuchsplanung, die Auslegung der Stimuli aus vorliegenden Messungen an Windparks, die Hörversuche selbst und die Auswertungen dieser in einem gesonderten Arbeits-Programm im Schalltechnischen Büro durchgeführt.
Die Ergebnisse der Arbeiten zur Richtcharakteristik der AM und des Doppler-Effektes bei WEA wurden im Rahmen einer Zusammenarbeit von Hochschulen und der TÜV Rheinland Energy GmbH gewonnen. Dies wurde auch möglich, weil der Betreiber der WEA ein offenes Ohr für Bildungszwecke hatte.
Wirkung der WEA-Geräusche auf Menschen
Aktuelle Untersuchungen legen nahe, dass die Wirkung der Geräuschimmissionen von WEA mittels logistischer Funktionen beschrieben werden kann. Aufbauend auf dieser Idee wird eine entsprechende Funktion hergeleitet und vorgestellt. Eingangsgrößen werden der Mittelungspegel LAeq sowie der messtechnisch erfasste und ausgewertete Parameter „pAM5“, dessen Bestimmung und Berechnung in der vorangegangenen Veröffentlichung [1] ausführlich beschrieben ist.
Eine grundlegende Dosis-Wirkungsbeziehung zur Beschreibung der Belästigung durch WEA- Geräusche wird in der Arbeit von Janssen S.A. et al [8] im Jahr 2011 aufgeführt.
Hier wird als Ergebnis von Untersuchungen mit N=1820 Teilnehmern in Schweden und in den Niederlanden eine Dosis-Wirkungs-Beziehung entwickelt, wie in Bild 1 beigefügt (FIG. 1 aus
[8]).
![Bild 1 Dosis-Wirkung-Beziehung zwischen Lden und der prozentualen Anzahl von belästigten Anwohnern (%A) und stark belästigten Anwohnern (%HA) außerhalb von Gebäuden aus [8].](https://www.ingenieur.de/wp-content/uploads/2020/12/X754-Bild1.jpg)
Bild 1 Dosis-Wirkung-Beziehung zwischen Lden und der prozentualen Anzahl von belästigten Anwohnern (%A) und stark belästigten Anwohnern (%HA) außerhalb von Gebäuden aus [8].
Algebraisch sind die o. a. Polynome wie folgt in [8] angegeben:
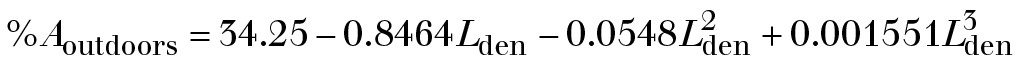 (1)
(1)
und
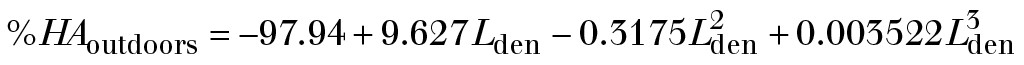 (2)
(2)
Anzumerken ist, dass bei den zugrunde liegenden Untersuchungen, die u. a. von E. Pedersen et al. schon seit 2003 durchgeführt wurden (z.B. [9] und [10]), das Thema AM (Amplitudenmodulation) nur indirekt erwähnt wird.
Eine weitere Studie zu dieser Thematik, bei der die AM unmittelbar eine Rolle spielt, ist die Arbeit von A. Bockstael et al. [11] aus dem Jahr 2012.
Die Ergebnisse beruhen auf Befragungen der Nachbarn im Umfeld von 3 WEA (Rotordurchmesser: 82 m, Nabenhöhe: 90 m und elektrische Nennleistung von Pel = 2 MW). Die WEA werden tagsüber im offenen Betriebsmodus und nachts aufgrund von Beschwerden im schall- und leistungsreduzierten Betriebsmodus (600 kW, max. 12 U/min) betrieben. Die Abstände betragen 300 m, 650 m und 1020 m zum wichtigsten Messpunkt bei einem der Nachbarn, wobei die WEA hintereinander aufgereiht in Richtung des genannten Messpunktes stehen. Die Abstände der anderen Nachbarn zu den WEA liegen in vergleichbaren Größenordnungen.
Die Befragungen der Anwohner erfolgten „Live“ mittels einer Web-App und in Anlehnung an den ISO-Standard ISO/TS15666:2003. Dabei konnten die Befragten während ca. 3 Monaten aktuell über ihr Empfinden mittels einer 5-stufigen Skala (– keine Belästigung, – leicht, – mittel, – hoch und – stark) Auskunft geben. Diese „direkte“ Bewertung führt nach Meinung der Autoren zu einem besseren Ergebnis als nachträgliche Befragungen aus dem Gedächtnis. Insgesamt konnten 552 Antworten von 3 Familien ausgewertet werden.
Im Ergebnis (vgl. Kapitel Nr. 4.3 aus [11]) werden diverse statistische Auswertungen zu dem ursprünglich angedachten Einflussparameter durchgeführt. Dabei korreliert die erklärte Belästigung mit dem Einfluss von Zustandsvariablen statistisch und kann mit Hilfe einer Gleichung quantifiziert werden. Grundgleichung ist die folgende logistische Funktion:
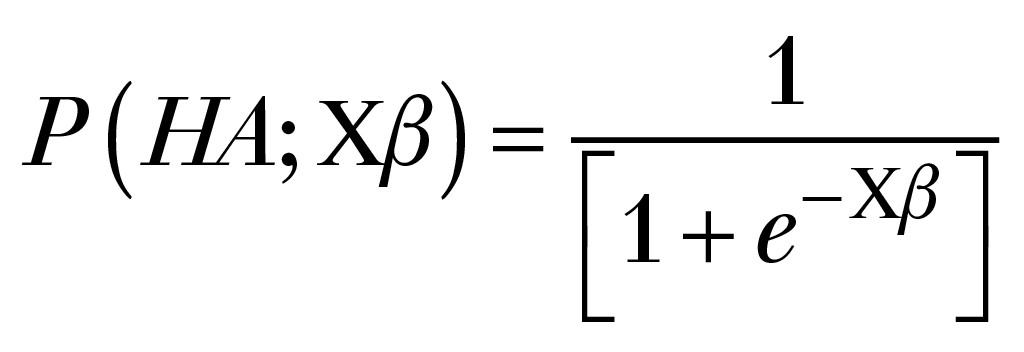 (3)
(3)
Die Variable Xß wird aus einer Linearkombination aus den Werten von simultan erfassten unabhängigen Parametern bestimmt. Eine Parameteranalyse führte zum Ergebnis, dass das Variablenpaar „Emissions-Schalldruckpegel Ls“ und ein „fluctuations indicator h“ in dB maßgebend sind. Letzterer wird dabei als normierte Amplitude der AM-Frequenz bestimmt und stellt ein Maß für die AM-Schwankungsbreite dar. Die statistisch ermittelte Gleichung (4) in der Studie [11] zur Bestimmung der Kenngröße Xb für die generell o. a. Gl. (3) lautet zum Schluss:
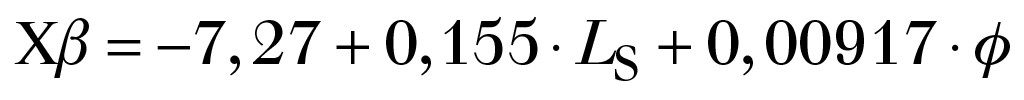 (4)
(4)
Dabei ist LS ein quellenbezogener Emissionspegel und h ein „Fluktuations-Indicator“ der von der Stärke der AM-Spektralkomponente abhängt. Diese Größen sind „sekundär“ in der Auswertung.
Die ersten statistischen Ergebnisse mussten in [11] uminterpretiert werden, um ein „operationelles“ Modell zur Vorhersage von starker Belästigung P(HA) zu erstellen, das Minderungsmaßnamen ermöglicht.
Ebenfalls aufbauend auf logistischen Funktionen vergleichen die Autoren Schäffer et al. in ihrer Studie [12] die Geräusche von WEA mit den Geräuschen des Straßenverkehrs (siehe auch [13]).
Dabei werden in den von ihnen durchgeführten Hörversuchen Stimuli mit und ohne AM angeboten. Weiterhin erfolgt eine Unterscheidung in periodisch oder zufällig („random“) auftretende AM.
Das Ergebnis ist eine Logit(pHA)-Funktion für die vorhergesagte Wahrscheinlichkeit von starker Belästigung (pHA) in der Form:
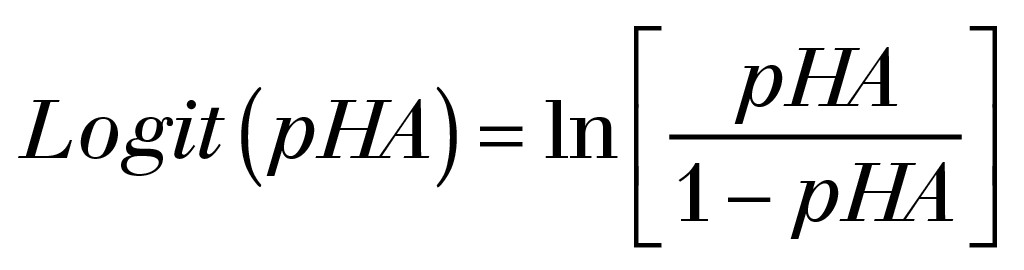 (5)
(5)
Die Funktion Logit(pHA) wird aus einer linearen Kombination von Einflussvariablen (Hauptvariable für die WEA stellt der Immissionspegel LAeq im Freien dar) bestimmt, deren Koeffizienten mittels Hörproben und Befragungen statistisch ermittelt werden. Ein interessantes Ergebnis der Probandenversuche ist, dass der Unterschied der zufälligen oder periodischen AM keinen großen Einfluss hat. Differenzen zeigen sich zwischen den Signalen mit oder ohne AM. Daraus ergeben sich bei der Untersuchung [12] zwei logistische Funktionen und zwar eine Basis-Funktion ohne AM und eine weitere Logit-Funktion mit AM.
Aus den Daten dieser Arbeit (Gl. 2 auf S. 2958 und Tabelle II auf S. 2957 aus [12]) lassen sich gemäß den Angaben der Autoren in ihrem statistischen Modell folgende Logit(pHA)-Funktionen annähernd ermitteln:
Ohne AM:
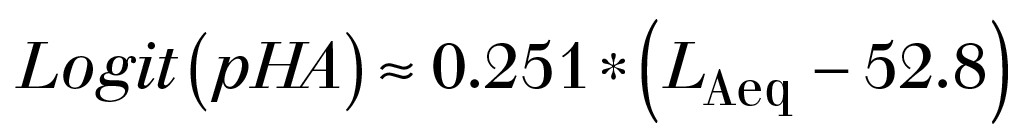 (6)
(6)
Mit AM:
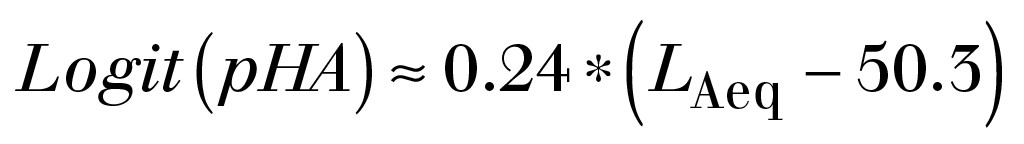 (7)
(7)
Trägt man die Funktionen grafisch auf, so ergeben sich die in Bild 2 aufgeführten Kurven für pHA in Abhängigkeit des LAeq.
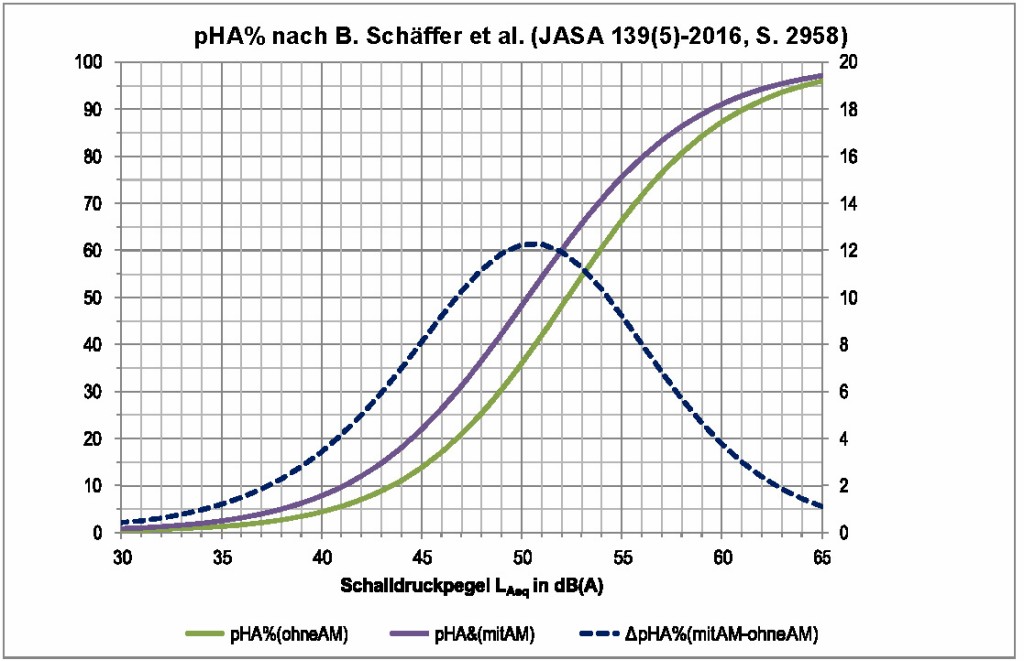
Bild 2 Grafische Darstellung der logistischen Funktionen pHA% aus den Gleichungen (6) grün und (7) lila, sowie deren Abweichungen DpHA% blau gestrichelt.
Foto: Autor
Die Funktionen erstrecken sich im Wesentlichen auf einen Bereich des Mittelungspegels LAeq von 30 dB(A) bis 65 dB(A) (vgl. [12]). Die logistische Verteilungsfunktion ohne AM erreicht den Wert von 50 % an stark belästigten Personen (pHA%) bei ca. 53 dB(A). Mit zusätzlicher AM sind bereits bei 50 dB(A) die Hälfte der Personen stark belästigt, also 3 dB „früher“. Durch AM entsteht demnach eine Erhöhung der Anzahl der stark belästigten Personen. Bei einem Mittelungspegel von LAeq = 50 dB(A) sind dies z. B. ∆pHA% = 12 mehr (vgl. blau gestrichelte Kurve).
Möchte man einen Vergleich zwischen den Bildern 1 und 2 herstellen, so kann man den Lnight als Vergleichsgröße zum LAeq aus dem Lden durch Abzug von ∆L~ 6 dB berechnen (Annahme: Die Anlagen laufen Tag und Nacht im gleichen Betriebszustand). Vergleicht man dann den Wert stark belästigter Personen ohne AM aus Bild 2 mit pHA% ≈ 22 bei 45 dB(A) mit einem Wert von pHA% ≈ 30 bei Lden = 51 dB(A) in Bild 1, so führen die beiden Untersuchungen zu ähnlichen Ergebnissen.
Die Darstellung entsprechend Bild 2 lässt die Hypothese zu, dass ausgehend von 30 dB(A) mit steigendem Schallpegel die AM zu einer wachsenden Störwirkung führt. Ab ca. 50 dB(A) ist dieser Einfluss wieder rückläufig. Es ist naheliegend, dass in der Praxis des Immissionsschutzes und bei Anwohnern in der Nähe von WEA Schalldruckpegel von LAeq ≥ 50 dB(A) (vor allem nachts) zu einer starken subjektiven Belästigung führen (unabhängig von der Frage der grundsätzlichen Genehmigungsfähigkeit). Die Aussage in Bild 2, dass in 50 % der Fälle eine starke Belästigung zu erwarten sei, ist durchaus plausibel. Vor diesem Hintergrund scheint eine Einschränkung des Bereiches auf Werte zwischen 30 dB(A) und 50 dB(A) sinnvoll für den Immissionsschutz zu sein.
Die Untersuchungsergebnisse [11] und [12] zeigen, dass durch das Auftreten von AM auch in Verbindung mit einer größeren Anzahl von WEA (Windparks), der gefundene Zusammenhang aus Bild 2 plausibel ist. Die Arbeit von A. Bockstael [11] führt zudem auf, dass neben dem LAeq als Parameter auch ein mit der AM gekoppelter Faktor eingeht. Über die Erkenntnisse aus Bild 2 hinaus ist demnach zu erwarten, dass auch die Stärke der AM z. B. in Form des Wertes pAM5-m (vgl. hierzu [1]) berücksichtigt werden müsste.
Herleitung der Belästigungsfunktion
Im Sinne der zuvor aufgeführten Erkenntnisse bietet es sich an, aus der Vielzahl an bestehenden Messdaten für Windparks (vgl. [1] und [14]) einen Vorschlag für eine Belästigungsfunktion P(A%;X) auszuarbeiten. Dabei wird ([2]) aufbauend auf [11] und [12] auf die verallgemeinerte Form der logistischen Funktion zurückgegriffen:
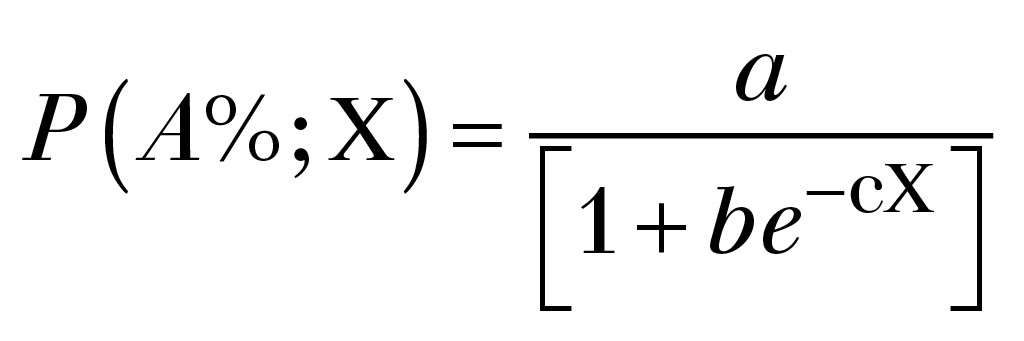 (8)
(8)
wobei die Parameter a, b und c anhand der vorliegenden Datensätze durch Anpassung ermittelt werden. Auf der Grundlage der Messdaten und ihrer Statistik aus [1] wird vorab von folgendem Zusammenhang für die Größe X ausgegangen:
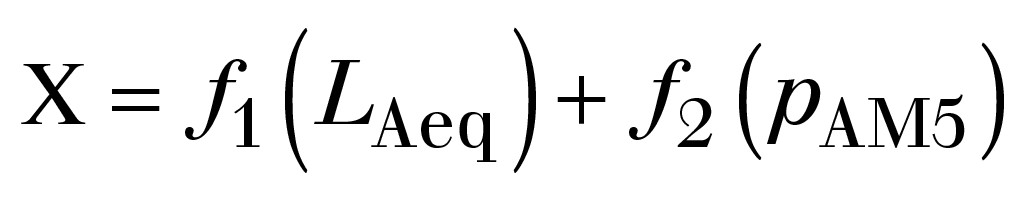 (9)
(9)
D. h. die Variable X ist die Summe aus linearen Funktionen der Größen LAeq (Mittelungspegel eines Zeitabschnittes) und pAM5 (AM-Schwankungsbreite eines Zeitabschnittes). Dies ist die Grundlage für die „Empfindungs“-Funktion P(A%;X) nach Gl. (8).
Auf Basis der Messergebnisse und Auswertungen aus [1], nämlich die Verteilungen LAeq (= pEM), pAM5 nach Bild 10 sowie die Daten für den LAeq aus Tabelle 2 (pEM-m anstelle von pEM ) sowie pAM5-m anstelle von pAM5) lassen sich folgende Funktionen f1 (LAeq) und f2(pAM5) (s. Gl.9) bilden:
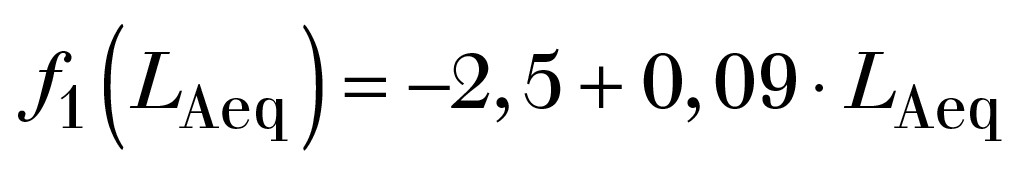 (10)
(10)
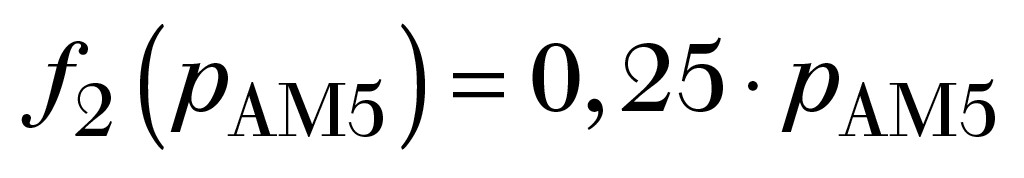 (11)
(11)
Mit den Funktionen (10) und (11) und den o. a. Messdaten, ergibt sich ein Satz von P(A%;X) Werte, abhängig von der Wahl der Konstanten a, b, c in Gl. (8). Die Analyse ergibt:
a = 0,97 b = 0,466·10² c = 2,631
Die Konstanten a, b und c der Gl. (8) werden hierbei durch Anwendung der Programm-Funktion „logsanp“ aus Math-CAD (vgl. Literaturhinweis in [1]) auf der Basis einer logistischen Verteilung bestimmt.
Die Berechnungen mit der somit entwickelten Funktion nach Gl. 8 und 9 (mit 10 und 11) ergeben die parametrische Darstellung in Bild 3 für die Funktion P(A%;X) für Werte des LAeq zwischen 30 bis 50 dB(A) und pAM5 zwischen 0 dB bis 6 dB. Man erkennt, dass die Kurven eine Ähnlichkeit mit der Darstellung nach Bild 2 aufweisen.
![Bild 3 Werte der Funktion P(A%;X) in Abhängigkeit der Variablen des Parameters X nach Gl. (8), (9),(10) und (11). Die „Punkte“ in dieser Darstellung ergeben sich gemäß Gl. (12) aus den „Messdaten“ nach Tabelle 2 aus [1].](https://www.ingenieur.de/wp-content/uploads/2020/12/X754-Bild3.jpg)
Bild 3 Werte der Funktion P(A%;X) in Abhängigkeit der Variablen des Parameters X nach Gl. (8), (9),(10) und (11). Die „Punkte“ in dieser Darstellung ergeben sich gemäß Gl. (12) aus den „Messdaten“ nach Tabelle 2 aus [1].
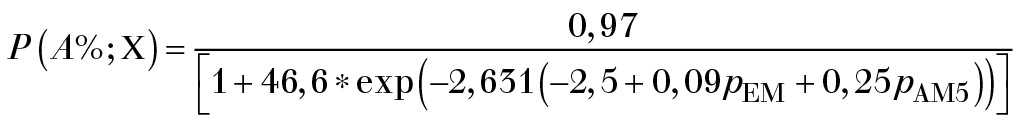 (12)
(12)
Validierung der Belästigungsfunktion durch Hörversuche
Zur Prüfung der hergeleiteten Belästigungsfunktion (s. Gl. 12) wurden Hörversuche an 10 Probanden durchgeführt. Bei den Probanden handelt es sich um Personen, die nicht durch die Geräusche von Windenergieanlagen belästigt sind. So ist für den Umfang der hier durchgeführten Hörversuche sichergestellt, dass die Ergebnisse nicht durch eine Vorprägung der Probanden beeinflusst werden. In diesem Zusammenhang sei z. B. auf die Veröffentlichung von J. Kastka et al. [15] hingewiesen, der für Fluglärmgeräusche zeigen konnte, dass aktive „Fluglärmgegner“ eine um ca. 20 dB höhere Empfindlichkeit gegenüber dem Lärm aufwiesen. Über ähnliche Einflüsse berichtet auch E. Pedersen et al [9,10].
In einem Vorversuch mit 3 Probanden wurde die zeitliche Dauer der Hörproben mit 25 Sekunden festgelegt. Die Auswahl der Soundfiles erfolgte anhand realer Messungen an 5 Immissionsorten.
Dabei wurden insgesamt 15 Hörproben mit unterschiedlichen Mittelungspegeln LAeq (= pEM) und Breite der Amplitudenmodulationen pAM5 ausgewählt. In der nachfolgenden Tabelle 1 sind für die 15 Messungen (= Hörproben) mit je 25 Sekunden die ermittelten, zugehörigen LAeq– und pAM5 – Werte sowie die Prognosewerte der Empfindungsfunktion P(A%;X) berechnet.
Legt man z. B. eine gleichmäßige 5-stufige Belästigungsskala (0 bis < 20%, 20 bis < 40%; usw.) zugrunde, dann setzt man eigentlich voraus, dass die Empfindungsfunktion und die damit verbundene Belästigung sowohl vom maßgebenden Wert des Immissionspegels LAeq als auch von der Bewertung der AM-Schwankungsbreite mit dem Wert pAM5 abhängen sollte.
Zur Durchführung der Hörproben wurde durch Vorversuche eine Skala von 0 bis 5 zur Einstufung der Belästigung als zielführend ermittelt. Danach wurden die rechnerischen Werte der Belästigungsfunktion P(A; X) auf eine Skala von 0 bis 5 skaliert. Diese skalierten Werte sind in der letzten Spalte P(A; X)skaliert der Tabelle 1 aufgeführt.
Diese Vorgehensweise ist an sich „alternativ“. In den Untersuchungen z. B. [11] und [12] werden die „Koeffizienten“ zu den Parametern der Belästigungsfunktion statistisch ermittelt. In unserem Fall wird aus dem vorgetragenen Vorwissen und Literaturrecherche die Belästigungsfunktion vorab „konstruiert“ und die Funktion mit den Versuchsergebnissen validiert.
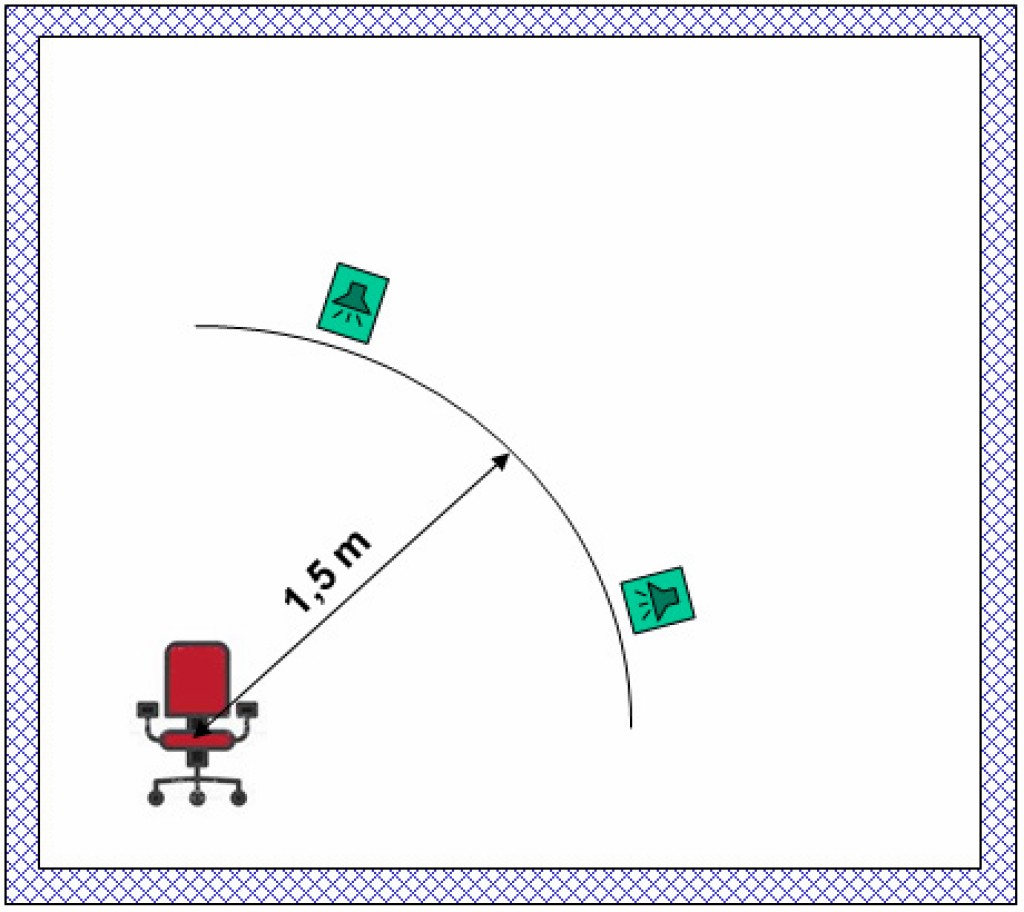
Die Hörproben wurden in einem reflexionsarmen Halbraum über Lautsprecher dargeboten, die in einem Abstand von 1,5 m zu den Probanden positioniert waren (siehe Bild 4).
Die Soundfiles wurden so eingepegelt, dass sie an der Hörerposition genau dem Mittelungspegel aus der Tabelle 1 entsprachen.
Den Probanden wurde im Hörversuch folgende Fragestellung vorgegeben: „Wenn das Geräusch vor Deinem Wohnhaus vorliegt, wie stark würde es Dich belästigen?“. Die Einordnung sollte auf einer Skala von 0 (nicht belästigt) bis 5 (stark belästigt) erfolgen.
Jedem Probanden wurden 5 feste Hörproben vorgegeben. Zusätzlich sollten 3 aus 10 möglichen weiteren Hörproben zufällig ergänzt werden. Die Proben durften ohne Vorgabe einer Reihenfolge beliebig oft abgespielt werden.
Zu Beginn des Hörversuches wurde jedem Probanden eine Hörprobe dargeboten, die einen Wert der skalierten Belästigungsfunktion von P(A; X)skaliert von ~ 0 aufwies. Dabei handelte es sich um ein Hintergrundgeräusch im Freien ohne Betrieb von Windkraftanlagen mit einem Mittelungspegel von LAeq = 26 dB(A).
Es wurden also in der Hauptauswertung insgesamt 90 Hörversuche durchgeführt.
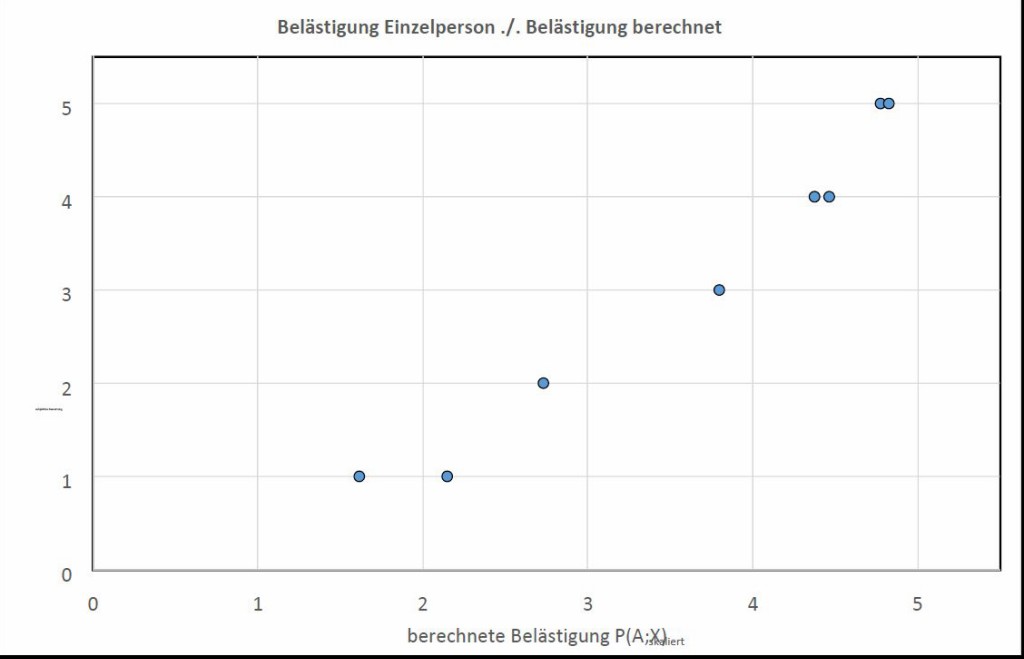
Bild 5 Gegenüberstellung der berechneten Belästigung P(A;X) und der subjektiven Bewertung eines Probanden.
Foto: Autor
Bild 5 zeigt die Auswertung eines einzelnen Probanden. Man erkennt, dass die subjektive Bewertung sehr gut der berechneten Belästigung entspricht.
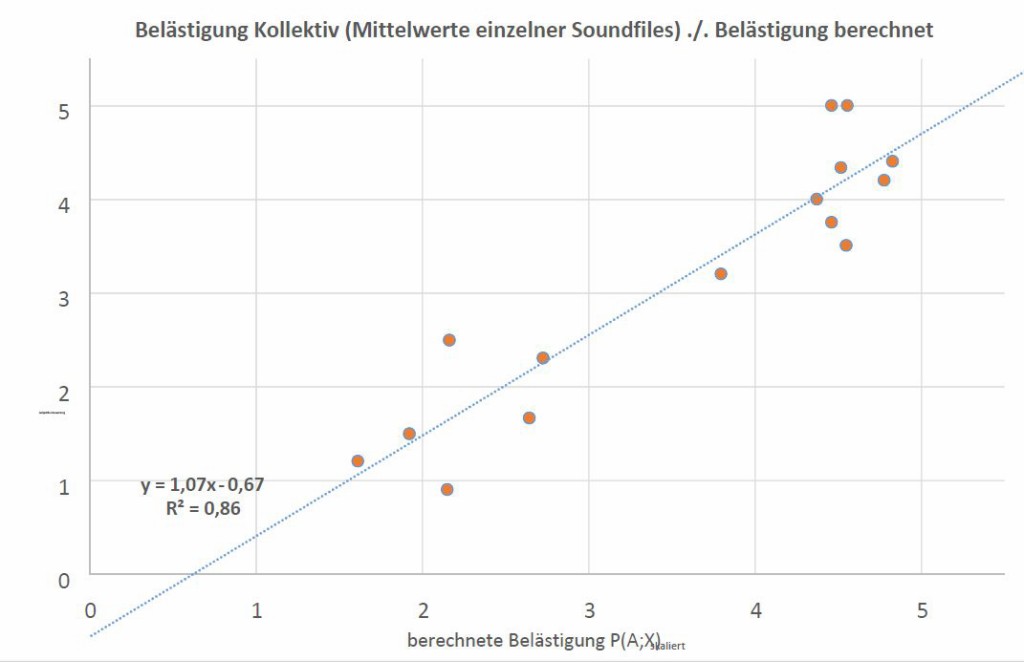
Bild 6 Gegenüberstellung der berechneten Belästigung P(A;X) und der Mittelwerte der subjektiven Bewertung von 10 Probanden der 15 Soundfiles.
Foto: Autor
Bild 6 stellt das Ergebnis des Kollektivs dar. Dabei wurden die Bewertungen für jeden der 15 Soundfiles gemittelt und aufgetragen. Hierbei zeigt sich, dass die Bewertungen der einzelnen Hörproben maximal um eine Bewertungsstufe von der berechneten Funktion abweichen.
Das Ergebnis zeigt, dass die gefundene Belästigungsfunktion (s. Gl. (12)) in Abhängigkeit der beiden akustischen Parameter LAeq und pAM5 abgebildet werden kann.
Die Ergebnisse der Untersuchungen nach [11] wurden dazu verwendet, operationell beim Betrieb eines Windparks Maßnahmen zur Senkung der Belästigung herauszuarbeiten.
Die Ergebnisse der Laborversuche nach [12] wurden gemäß den Angaben in der Arbeit [13] zur Erstellung eines Verfahrens zur Beurteilung von Geräuschimmissionen von WEA in der Schweiz herangezogen, bei dem die AM als eine Variante der Impulshaltigkeit berücksichtigt wird und ein Zuschlag im Beurteilungsverfahren auslösen kann.
In der englischen Studie [16] wird empfohlen die AM mit der Methode von IOA zu bestimmen und zu bewerten. Danach ist ein Zuschlagsystem zur Beurteilung vorgesehen, abgestuft in Stufen von 3 dB ab einem Schwellenwert der AM bis zu 5 dB bei sehr hohen AM Werten.
Diese ergänzenden Erkenntnisse können auch unter dem Gesichtspunkt verstanden werden, dass eine Beurteilung der WEA Geräusche nicht schlicht auf einem Vergleich von Langzeitmittelwerten mit Langzeitgrenzwerten reduziert werden darf. Dies ist inzwischen allgemeiner Konsens, der bei vielen Geräuscharten und Geräuschquellen zu einer wirkungsvollen Entwicklung von Lärmminderungsstrategien und –instrumenten geführt hat.
Unser Ansatz (s. Gl. 12) ist unter diesen Gesichtspunkten „operationell“ voll dazu fähig, wirksame Lärmminderung zu ermöglichen.
Richtcharakteristik der AM bei Windenergieanlagen [3]
In diesem Kapitel wird über ein weiteres Vorhaben berichtet, die Richtungsabhängigkeit der AM bei Windenergieanlagen empirisch zu untersuchen [3]. Die Vermutung hierbei geht dahin, dass Anwohner AM wahrnehmen, trotz ausreichender Entfernung zum Windpark. Grund hierfür ist u. a. die Richtungsabhängigkeit der AM. Dieses ist nicht mit der Richtcharakteristik der WEA nach DIN EN 61400-11 [5] zu verwechseln.
Ausgangspunkt dieser Vermutung sind einerseits theoretische Überlegungen, z. B. aus der Arbeit [17] oder weitere Hinweise aus den Untersuchungen von S. Oerlemans in [7] (Work Package 1). Die Hypothese ist: die AM quer zur Rotorebene der WEA ist stärker ausgeprägt als die AM vor oder hinter der Rotorebene.
Hierfür werden Messungen an einer einzelnen WEA ausgeführt und die Daten werden im Sinne dieser Hypothese analysiert [3]. Die Vorbereitung der Messungen, die Messungen selbst und die darauf folgende Datenauswertung und Interpretation orientieren sich, sofern erforderlich bzw. möglich, an den Vorgaben der Norm [5]. Ein wichtiger Aspekt hierbei ist, dass bei WEA die aerodynamischen Geräusche der Rotorblätter dominieren, insbesondere nahe den Rotorblattspitzen. Dieses ist auf die hohen Geschwindigkeiten zurückzuführen, die leistungsstarke WEA an den Rotorblattspitzen erreichen. Aufgrund der drei Rotorblätter sowie der relativ hohen Drehzahl der WEA werden die aeroakustischen Schallemissionen als sich wiederholendes Rauschen wahrgenommen. Solch ein Rauschen wird vom menschlichen Gehör als Lärm empfunden und in der Literatur als AM bezeichnet [3].
Gestaltung der Feldmessungen [3]
Die für die ausgeführte Messung relevante WEA ist Teil eines Windparks bestehend aus insgesamt 7 WEA gleichen Typs. Auf eine Darstellung von produkt- und standortspezifischen Details wird hier aber verzichtet. Die ausgewählte WEA befand sich als letzte der Kette in einer optimalen fremdgeräusch- bzw. störungsfreien Position. Die Turmhöhe beträgt 142,5 m, der Rotordurchmesser 113 m und die Nennleistung der WEA beträgt 3 MW. Die Nenndrehzahl ist 14 Umdrehungen pro Minute.
Zu den am 13.11.2018 ausgeführten Messungen wurden spezifische Daten des Herstellers zur Verfügung gestellt (Schallemissionskenndaten, Herstellerbescheinigung). Außerdem wurden über die Fernüberwachung vor, während und nach dem Zeitpunkt der Messungen 10 Minuten-Mittelwerte der elektrischen Leistung der vermessenen WEA, Rotordrehzahl, Windgeschwindigkeit in Gondelhöhe, Azimutwinkel der Gondel sowie Blattwinkel der einzelnen Rotorblätter mitgeteilt. Es erfolgte auch eine Synchronisation aller Messgeräte untereinander und mit der WEA. Bei den Messungen wurde neben den akustischen Messsystemen eine eigene Wetterstation (Höhe 10 m über Boden) aufgebaut um Luftdruck, Lufttemperatur, Luftfeuchte, Windrichtung und Windgeschwindigkeit im 10 Sekunden Takt zu erfassen. Über die eigentliche Messzeit (s. Tabelle 2) ergaben sich folgende Betriebsdaten bzw. Wetterdaten:
Lufttemperatur 9,1 ± 0,3 °C
Luftdruck 961 ± 0,5 hPa
Luftfeuchte 80 %
Windgeschwindigkeit in 10 m Höhe: 6,9 ± 0,7 m/s
Turbulenzgrad ca. 15 %
Windgeschwindigkeit in Gondelhöhe (h=142m): 9 ± 0,9 m/s
Elektrische Leistung der WEA 1970 ± 400 kW
Rotordrehzahl 13,5 ± 0,6 Umin-1
Blattwinkel –1,15 ± 0,8 Grad
In einer ausführlichen Messvorbereitung vor Beginn der Messungen wurden drei Messpunkte um die WEA festgelegt. Dies war ein Kompromiss zwischen den Zielen der Messungen und den organisatorischen Bedingungen des Vorhabens. Die Messplanung sah vor, den Referenzmesspunkt nach [5] im Lee der WEA im Dauerbetrieb arbeiten zu lassen. Das zweite Messsystem wurde abwechselnd während mindestens 30 Auswerteminuten entweder seitlich der WEA (Querposition Q, annähernd 90 °+) und vor der WEA (Vorne V45 °) positioniert. Andere Punkte im Lee waren leider nicht zugänglich (Jungtiere auf der Weide). Die Lage der Messpunkte ist schematisch in Bild 7 angegeben.
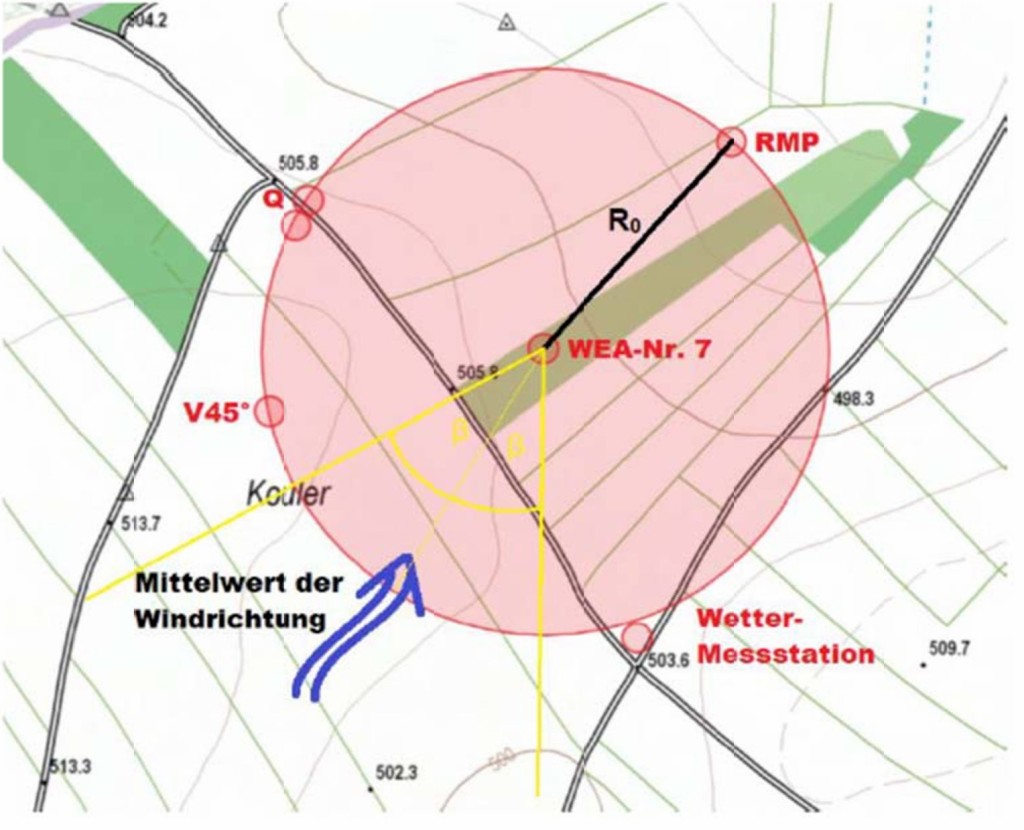
Bild 7 Die zu messende Windenergieanlage (Nr. 7) inklusive eingezeichnete Messpunkte (Draufsicht). Der Messabstand betrug einheitlich 170 m zum Turm. Die Geländehöhenunterschiede wurden bei der Auswertung berücksichtigt. Die benachbarte WEA (Nr. 6) im Osten war ausreichend entfernt, so dass ihr Einfluss auf diese Messungen vernachlässigt werden kann.
Foto: Autor
Bild 8 zeigt den Windpark aus der Sicht der vermessenen WEA.
Wie bereits angegeben konnten zwei amtlich geeichte Schallpegelmesser verwendet werden.
Der Referenzmesspunkt RMP nach [5] wurde auf die eigene schallharte Bodenplatte gestellt und arbeitete somit messtechnisch als ein Grenzflächenmikrofon mit Sekundärwindschirm. Das zweite Mikrofon konnte nicht so betrieben werden und wurde mit Sekundärwindschirm auf einem Stativ im 4 m Höhe über Boden aufgestellt. Dementsprechend sind bei der Auswertung der Daten die unterschiedlichen Schallreflexionen der Bodenplatte ( 6 dB) und des Stativs (3 dB) zu berücksichtigen.Folgende Daten wurden von beiden Schallpegelmessern simultan erfasst:
LAF(t), LAeq,100ms(t), LAS(t) in 100 ms Takt (sog. Schnellprotokoll Gesamtpegel)
Leq(1s) / LAeq(1s) in Terzbandbreite von 6 Hz bis 20 kHz
Wave-Dateien in 10 Minuten Blöcke, 48 kHz
Für diese Auswertung war vorgesehen, einerseits die AM aus den Messdaten zum A-Gesamtpegel zu bestimmen, nachdem manuell die protokollierten Störungen aus den Messdaten entfernt wurden. Außerdem sollte aus den Sekunden-Werten eine Auswertung in Anlehnung an [5] zur Ermittlung der Richtcharakteristik der WEA im A-Gesamtpegel erfolgen, um beide Effekte miteinander vergleichen zu können. Die weiteren Ergebnisse z. B. Terzbandbreite bzw. aus einem „Resampling“ der Wave- Dateien (Postprocessing) als Schmalbandanalysen werden bei anderen Fragestellungen untersucht.
Auswertung der Feldmessungen zur Richtungsabhängigkeit und Richtwirkung [3]
Die Tabelle 2 enthält die Zeitfenster der Daten für die hier durchgeführten Auswertungen.
Ein typisches Beispiel der gemessenen Pegelzeitverläufe (100 ms Takt) ist den Bildern 9, 10, 11 und 12 zu entnehmen.
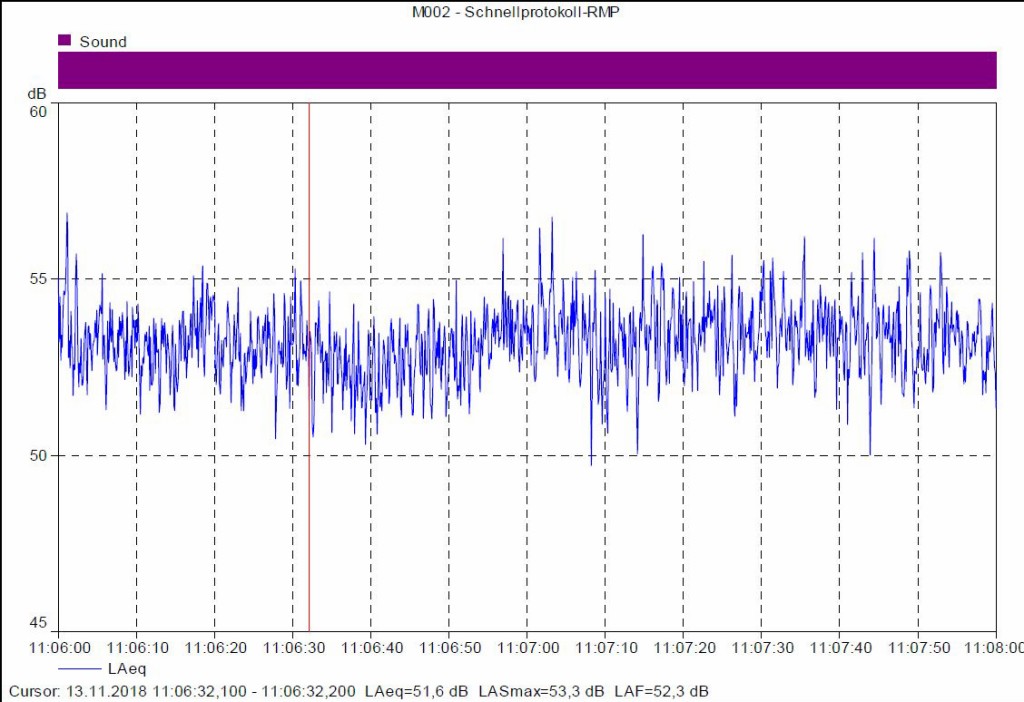
Bild 9 Pegelzeitverlauf LAeq, 100ms(t) am RMP in der Zeit von 11:06 bis 11:08. Auflösung 100 ms-Takt.
Foto: Autor
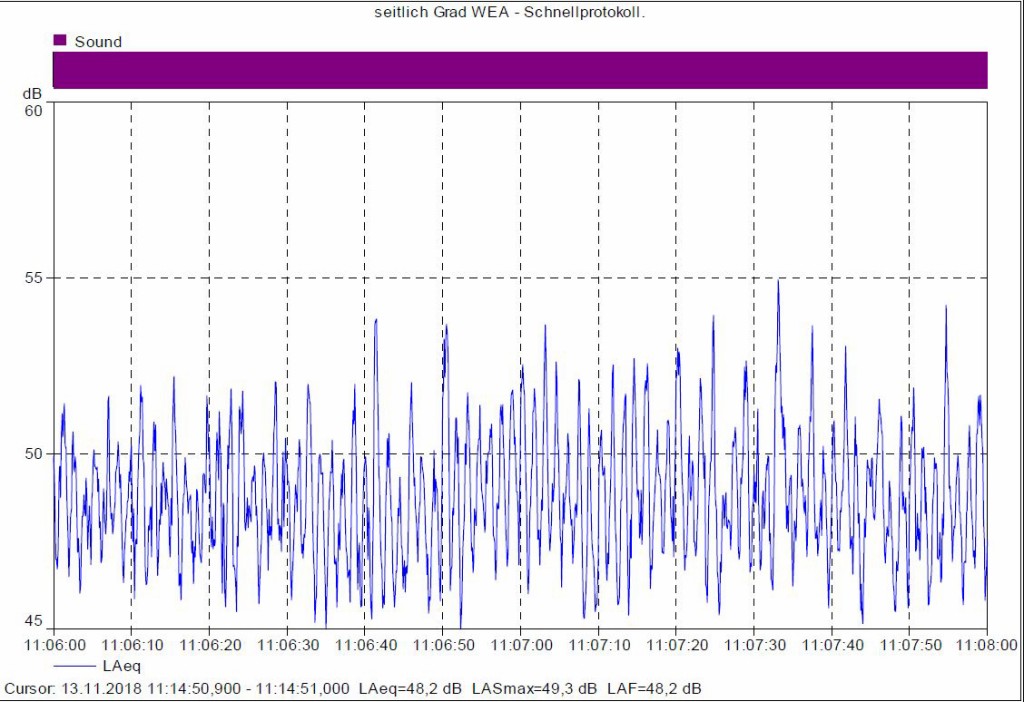
Bild 10 Pegelzeitverlauf LAeq, 100ms(t) am Messpunkt Q(uer) in der Zeit von 11:06 bis 11:08. Auflösung 100 ms-Takt.
Foto: Autor
Die Bilder 9 und 10 zeigen simultan gemessene A-Schallpegel jeweils am Referenzmesspunkt RMP und am Messpunkt seitlich (Q).
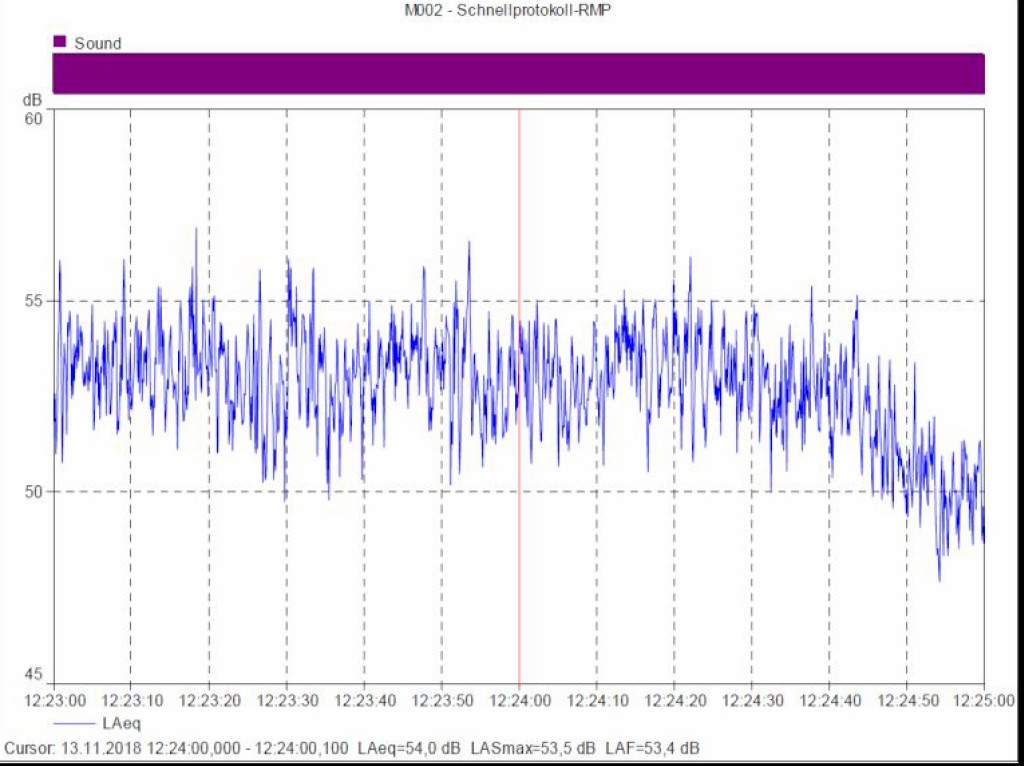
Bild 11 Pegelzeitverlauf LAeq, 100ms(t) am RMP in der Zeit von 12:23 bis 12:25. Auflösung 100 ms-Takt.
Foto: Autor
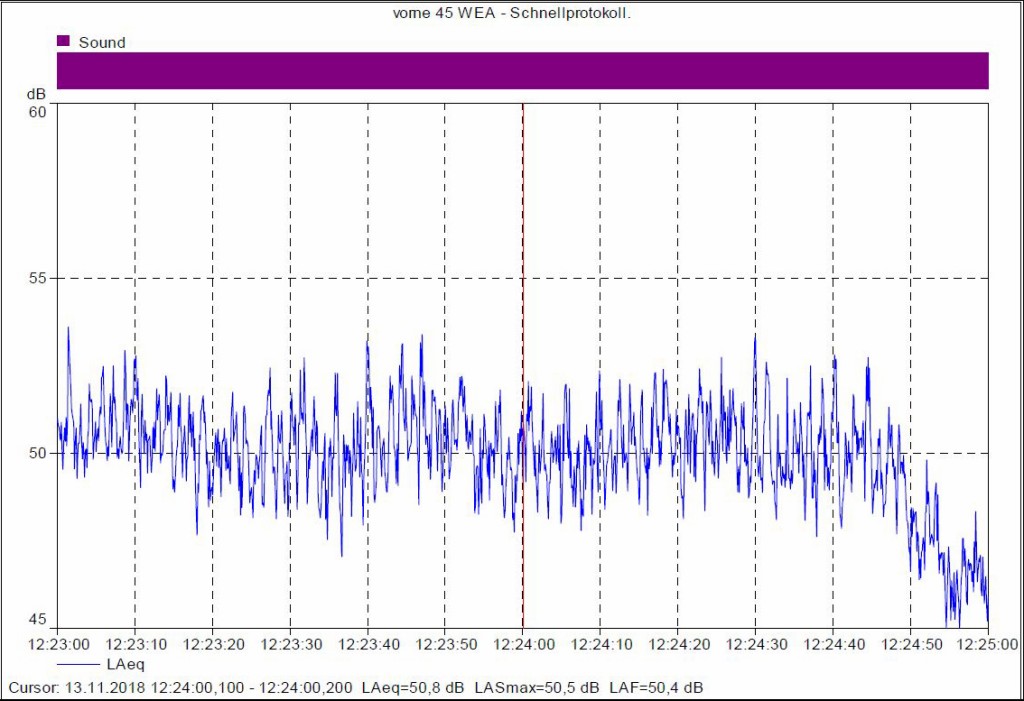
Bild 12 Pegelzeitverlauf LAeq, 100ms(t) am Messpunkt vorne, V45 in der Zeit von 12:23 bis 12:25. Auflösung 100 ms-Takt.
Foto: Autor
Die Bilder 11 und 12 zeigen in ähnlicher Art die simultanen Pegelzeitverläufe am RMP und am Messpunkt vorne V45.
Beim Vergleich der Bilder 9, 11 und 12 ist zu erkennen, dass die AM der verschiedenen Messpositionen relativ gleichmäßig verlaufen. Es ist aber deutlich, dass die Breite der AM bei der Position Q (seitlich) (Bild 10) deutlich stärker ist als hinten (RMP) (Bild 9, 11) oder vorne (V45) (Bild 12). Dies untermauert die Hypothese, dass die AM seitlich stärker ist als in den anderen Richtungen.
Zur Bestimmung der AM-Schwankungsbreite wurde in [3] übungshalber mit dem Auswerteverfahren nach A. Fukushima et al [18] gearbeitet. Etwas in Abweichung von [18] wurden die Zeitreihen
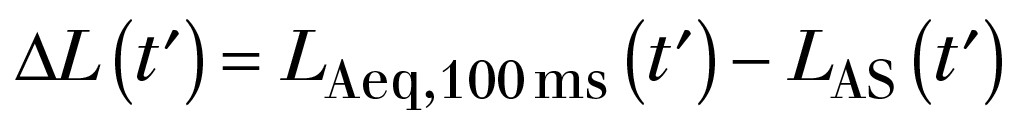 (13)
(13)
anstelle der japanische Version mit LAF(t‘) in 50 ms Takt gebildet. Diverse Überlegungen zeigen, dass sich durch diese Veränderung keine gravierenden Unterschiede ergeben, vor allem im Vergleich zum Wavelet-Verfahren nach [1]. Jede Minute entstand also eine eigene Zeitreihe DL(t‘), sowohl für die Daten am RMP als auch in den anderen Richtungen entsprechend den Zeitintervallen nach Tabelle 2. Aus der jeweiligen Verteilung der DL(t‘)-Werte in jede Minute wurden die Quantile DL97,5% und DL2,5% ermittelt und daraus der Wert AM(t) der jeweiligen Minute gebildet.
Es gilt also je Minute:
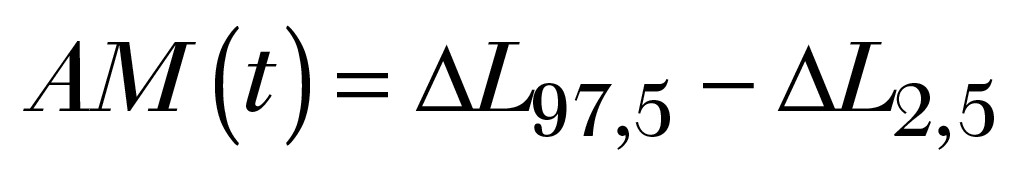 (14)
(14)
Somit ergeben sich am RMP n=119 Werte, am Messpunkt Q n=85 Werte und am Messpunkt V45 n=34 Werte.
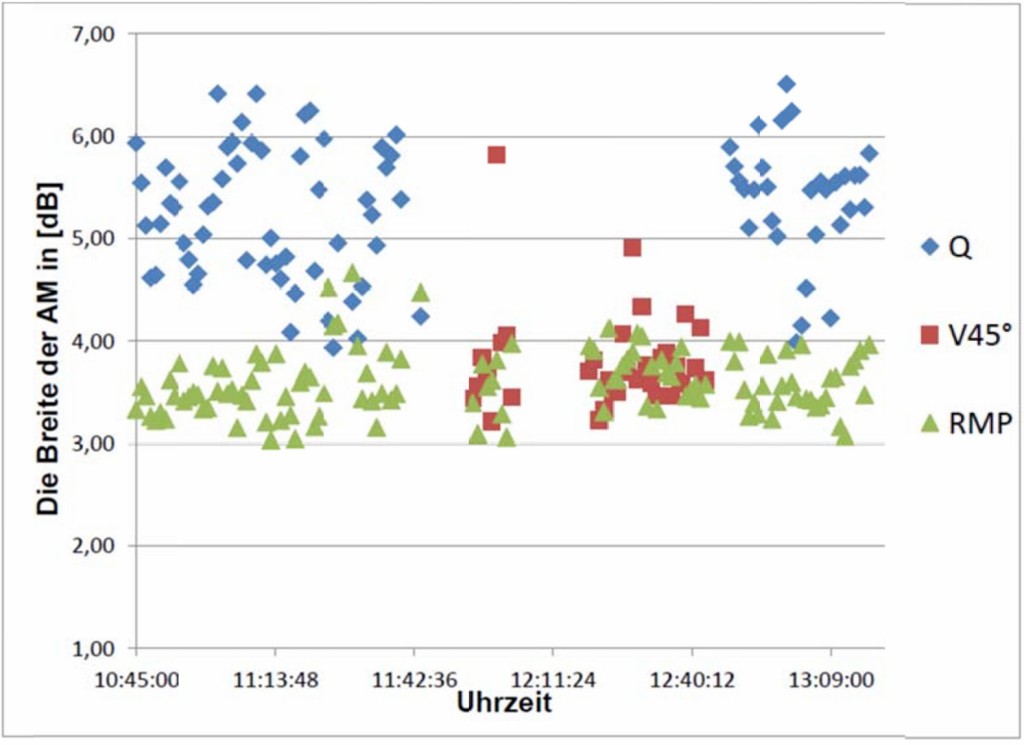
Bild 13 Darstellung der gemessenen AM(t)-Breiten nach Gl. 14 an den verschiedenen Messpositionen. Es handelt sich jeweils um ‧simultane Messdaten.
Foto: Autor
In Bild 13 sind diese Werte zusammenfassend dargestellt.
Es ergibt sich im Mittel folgende Tendenz für die simultan gemessene Breite der AM:
AM-Seite (Q): 5,29 dB ; AM Hinten: 3,56 dB bei n = 85 Werte
AM-Vorne (V45) : 3,79 dB ; AM-Hinten: 3,65 dB bei n= 34 Werte
Ein Differenzen-Test liefert die zusätzliche Auskunft, dass die mittlere Differenz
AM-Seite (Q) – AM Hinten &1,7 dB
statistisch signifikant ist. Das ist nicht der Fall bezüglich der Differenz AM-Vorne(V45) – AM Hinten.
Damit kann ausgesagt werden, dass die AM seitlich deutlich stärker ausgeprägt ist als hinter oder vor der WEA.
Natürlich ist es interessant zu wissen, wie es sich bei größeren Entfernungen mit dieser Richtungsabhängigkeit verhält. Eine Aussage dazu ist eigentlich nur möglich, wenn man differenziert auf die Beiträge zur AM eingeht und ihre Richtungs- und Abstandsabhängigkeit in Erwägung zieht. Eine Teilantwort zu suchen ist Gegenstand des dritten Teils dieser Studie. Die weitere Auswertung der Messdaten lief auf eine Bestimmung der Richtcharakteristik der Schallabstrahlung der WEA in horizontaler Richtung und an den ausgewählten Messpunkten für diese Untersuchung hinaus.
Basiswert ist hierbei der Abstand von 170 m horizontal. Die Auswertung der simultanen Messdaten erlaubt selbst bei der hohen Leistung der WEA absolut nur eine angenäherte Aussage, da eine strenge Fremdgeräuschkorrektur durch Abschaltung nicht ausgeführt wurde. Dennoch ist die Annahme berechtigt – da hierfür in der Norm [5] und bei simultanen Messungen letztlich die Fremdgeräuschkorrektur paarweise entfällt -, dass die gemessenen Pegel-Differenzen aussagefähig sind. Es wurden jedoch die durch das Gelände erforderlichen Entfernungskorrekturen nach [5] durchgeführt und auch der o. a. Unterschied in der Aufstellung der Mikrofone berücksichtigt. Somit ergab sich im Mittel jeweils ein Ausgangswert zur Bestimmung des Schalleistungspegels. Dieser lag im Mittel insbesondere am RMP in guter Übereinstimmung mit den zertifizierten Werten (dreifach Vermessungen nach [5] und [6]) bei der untersuchten WEA.
Die Auswertung zur Richtcharakteristik (Anzahl der Datenpaare wie bei der AM) ergibt folgende richtungsabhängige Pegeldifferenzen:
LAeq-seitlich(Q) – LAeq-RMP = – 1,33 dB (statistisch signifikant)
LAeq-vorn(V45) – LAeq-RMP = 0,48 dB (statistisch signifikant)
Dieses Ergebnis ist vor allem interessant, weil es zwei gegenläufigen Tendenzen offenbart. Einerseits ist die Geräuschemission seitlich etwas geringer als in den anderen Richtungen. Andererseits ist die AM-Schwankungsbreite in seitlicher Richtung deutlich stärker als in den anderen Richtungen.
Auswertung zur frequenzabhängigen Richtcharakteristik
In einer ergänzenden Untersuchung zu der Arbeit [3] wurde auf der Basis der in Terzbandbreite erfassten Schalldruckpegel übersichtsmäßig auf die Frequenzabhängigkeit der Richtcharakteristik der WEA näher eingegangen. Bei der Auswertung beschränken wir uns auf die Messergebnisse am Messpunkt RMP und am Messpunkt seitlich (Q) ohne zusätzliche Korrekturen bezüglich der Aufstellung des Mikrofons bzw. der geringen Höhenunterschiede des Geländes. In der Auswertung wurden die erfassten LZeq Sekundenwerte in Terzbandbreite jeweils zu Minuten-Mittelwerte zusammengefasst und aus diesem Datensatz (Minutenmittelwerte) nach dem in der Arbeit [19] angegebenen Verfahren die Perzentil-Spektren – Ordnungsgröße ist der Betrag von LZeq (Gesamt)) – während der angegebenen Messzeit errechnet. Gemäß den vom Betreiber der WEA mitgeteilten Ergebnissen (10 Minuten Mittelwerte der WEA-Betriebsgrößen) betrug die elektrische Leistung der WEA während der Messdauer 1970 ± 400 kW.
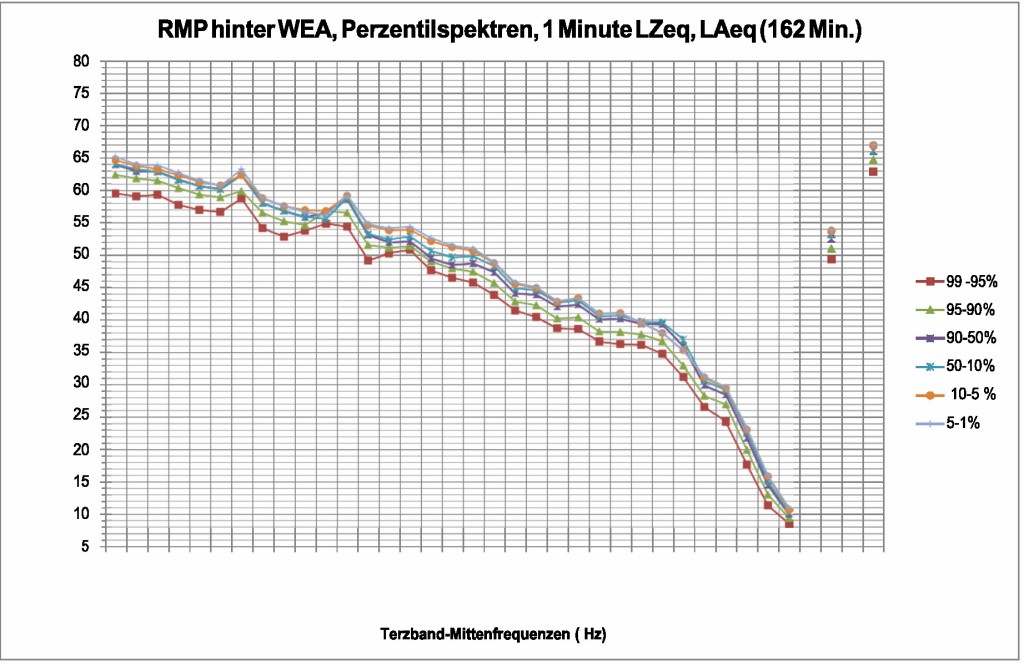
Bild 14 Perzentil-Spektren LZeq am RMP während der Messungen am 13.11.2018. Man beachte den annähernd linearen Abfall der mittleren Terzbandpegel im Frequenzbereich zwischen 160 Hz und ca. 2 kHz. Bei höheren Frequenzen nimmt der gemessene Emissionspegel im Terzbandbereich stärker mit der Frequenz ab. Die Spannweite im A-Gesamtpegel beträgt knapp 4,5 dB(A). Der Bereich unter 250 Hz wird gesondert in Bild 15 dargestellt.
Foto: Autor
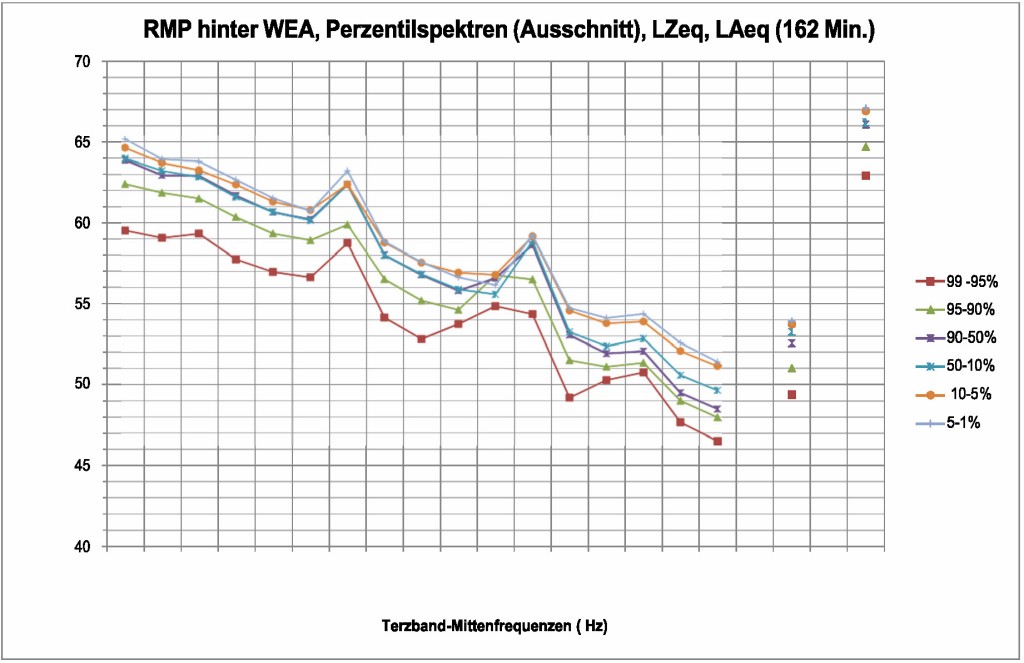
Bild 15 Perzentil-Spektren LZeq am RMP während der Messungen am 13.11.2018. Ausschnitt im Frequenzbereich 6,3 Hz bis 250 Hz. Man beachte den im Mittel annähernd linearen Abfall über alle Frequenzen. In den Terzbändern 25 Hz, 63 Hz und 80 Hz treten tonhaltige Beiträge auf, die im Bereich 63 Hz und 80Hz ‧abhängig von der Rotordrehzahl sind.
Die Bilder 14 und 15 für den Messpunkt RMP und die Bilder 16 und 17 für den Messpunkt seitlich (Q) stellen diese weiteren Ergebnisse graphisch dar.
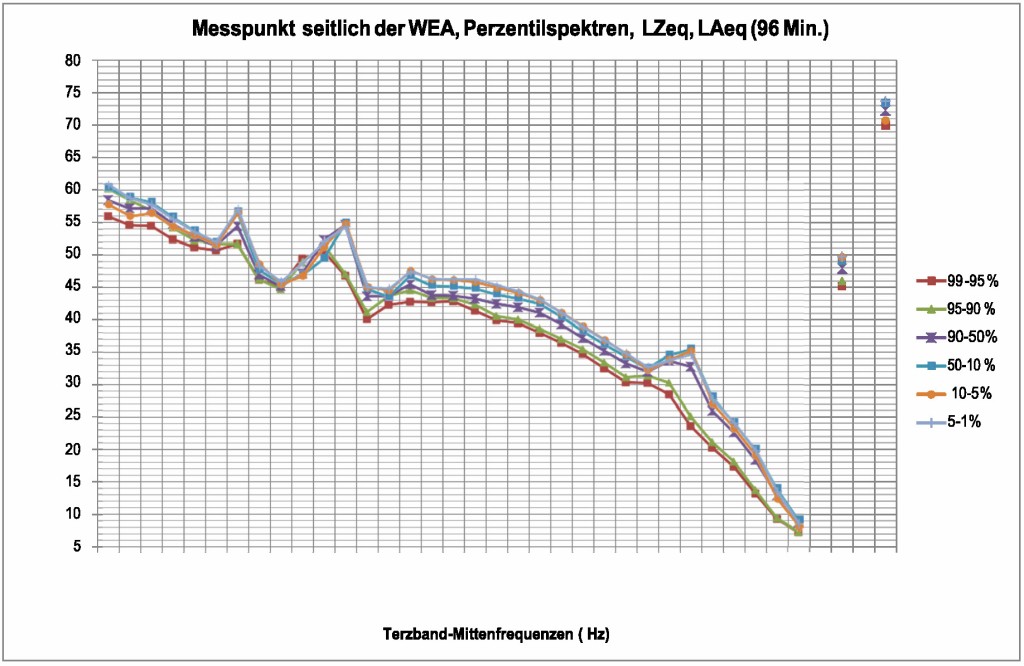
Bild 16 Perzentil-Spektren LZeq am Messpunkt seitlich (Q) während der Messungen am 13.11.2018. Man beachte, dass im mittleren Frequenzbereich zwischen 100 Hz und 800 Hz der Pegel weniger stark mit der Frequenz abnimmt als am Messpunkt RMP (Vgl. Bild 14). Außerdem treten bei höherer Leistung der WEA (Perzentil 90-50 %) hochfrequente Anteile bei 2,5 kHz und 3,15 kHz auf. Das ist kein Fremdgeräusch sondern eine eigene Komponente des Geräusches der Rotorblätter im Nahbereich. Die Spannweite im A-Gesamtpegel beträgt knapp 4,5 dB(A). Der Bereich unter 250 Hz wird gesondert in Bild 17 dargestellt.
Foto: Autor
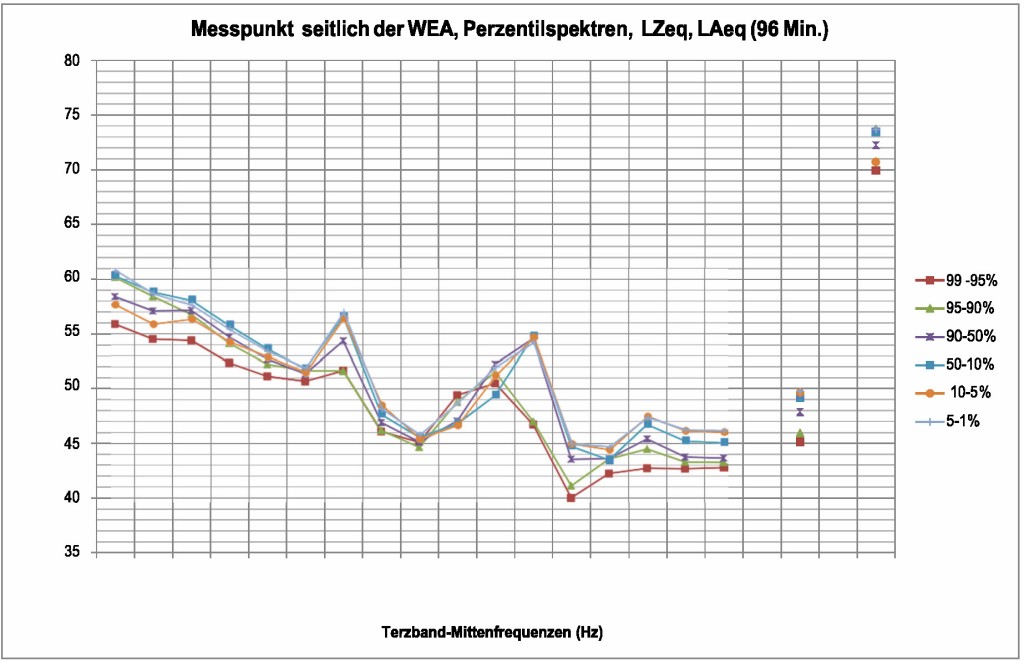
Bild 17 Perzentil-Spektren LZeq am Messpunkt seitlich (Q) während der Messungen am 13.11.2018. Ausschnitt im Frequenzbereich 6,3 Hz bis 250 Hz. Man beachte im Bereich über 100 Hz, dass der Pegel nicht mit der Frequenz abnimmt. In den Terzbändern 25 Hz, 50 Hz, 63 Hz und 80 Hz treten tonhaltige Beiträge auf, die im Bereich 50 Hz, 63 Hz und 80Hz offenkundig von der Rotor‧drehzahl abhängig teilweise gleichzeitig auftreten. Die im nächsten Abschnitt durchgeführten Schmalbandanalysen werden diesen Sachverhalt näher erläutern.
Foto: Autor
Die Bilder 14–15 und 16–17 stammen zwar aus paarweise simultan gemessenen Einzelwerten (Mittelwerte über 1 Minute Dauer), aber diese statistische Betrachtung hebt die strenge Gleichzeitigkeit gewissermaßen auf.
Aus diesen Ergebnissen folgt auch die Einsicht, dass die gegensätzliche Richtungsabhängigkeit der Pegelabstrahlung insgesamt und der Amplitudenmodulation auf Mechanismen in der Geräuschemission hinweisen, die man bisher zu undifferenziert betrachtet hat. Um bei diesen Fragestellungen weiter zu kommen, wird im nächsten Abschnitt das Instrumentarium der Schmalbandanalyse eingeführt.
AM bei WEA und Doppler-Effekt [4]
In diesem Kapitel wird u. a. über die Untersuchungen im Vorhaben [4] berichtet. In der Arbeit [4] wurde bezüglich der Geräuschemissionen der WEA der Fokus auf die o. a. ambivalente Eigenschaft dieser Geräuschquelle gelegt. Sie ist in einem gewissen Sinne stationär, ja ortsfest. In einem anderen Kontext aber ist sie beweglich. Jedermann der in der Nähe einer WEA deren Akustik ausgesetzt ist, wird unweigerlich damit konfrontiert. Eine Charakteristik von „schnellen bewegten Quellen“ ist nämlich der Doppler-Effekt. Daher wurde bei dieser Arbeit der Schwerpunkt der Untersuchungen auf den Doppler-Effekt gerichtet. Ein Ziel der Untersuchung war durch eigene Messungen den Doppler- Effekt bei WEA zu „erfassen“ und zu interpretieren.
Zunächst werden die Arbeiten zu Erfassung und Verarbeitung von Messdaten erörtert, um mit dem Instrumentarium der Schmalbandanalyse, Sonogramme, etc. den Schall einer bewegten Quelle zu erfassen. Anschließend wird die aus der theoretischen Modellierung des WEA-Geräusches zugängliche Wirkung des Doppler-Effektes untersucht, die durch Messungen ohne Arrays erfasst werden könnte. Zum Schluss werden die aus Messdaten herausgearbeiteten Effekte quantitativ erörtert.
Messdaten und Auswerteverfahren
Die Messungen in [4] erfolgten gemeinsam mit den Untersuchungen der o. a. Arbeit [3]. So ergab sich die bereits angegebene Messkonfiguration, die gleichen drei Messpunkte nach Bild 7 und die Messdaten wurden innerhalb der in der Tabelle 2 angegebenen Zeitfenster paarweise zeitgleich erfasst. Die Besonderheit ist, dass zusätzlich zu den üblichen Auswertungen über die Schallpegelmesser und weitere Software in [3], in dieser Arbeit die simultan erfassten Wav-Dateien mittels Schmalbandanalyse bearbeitet wurden.
Die Wav-Dateien lagen systematisch in synchronisierten Blöcken von 10 Minuten Dauer vor. Das post- processing erfolgte mit der Technik des Mess-Systems Samurai (Sinus Messtechnik) wobei die Schmalbandanalysen über den gesamten erfassten Messbereich durchgeführt wurden. Zusätzlich zu der üblichen FFT-Analyse wurde auch die Option 1/48-Oktave für die Schmalbandanalyse herangezogen. Daraus konnten Sonogramme erstellt und nach Datenexport weitere Analysen des Pegelzeitverlaufes in dieser variablen Schmalbandbreite erfolgen. Ziel der Vorarbeiten in [4] war es, ein Mindestmaß an „Feinauflösung“ zu erreichen, sowohl zeitlich (zu 125 ms Takt hin) als auch frequenzabhängig, insbesondere bei niedrigen Frequenzen, um den Doppler-Effekt ohne Arrays zu messen.
Die Methodik der Verarbeitung der Wav-Dateien gestaltete sich in der Arbeit [4] nicht einfach, zumal bei den Messungen Unterschiede in der Aufnahmemethode auftraten, so dass erst im post- processing eine paarweise Vergleichbarkeit der Daten je Messpunkt (vgl. die o. a. Gleichzeitigkeit der Messungen in [3]) möglich wurde.
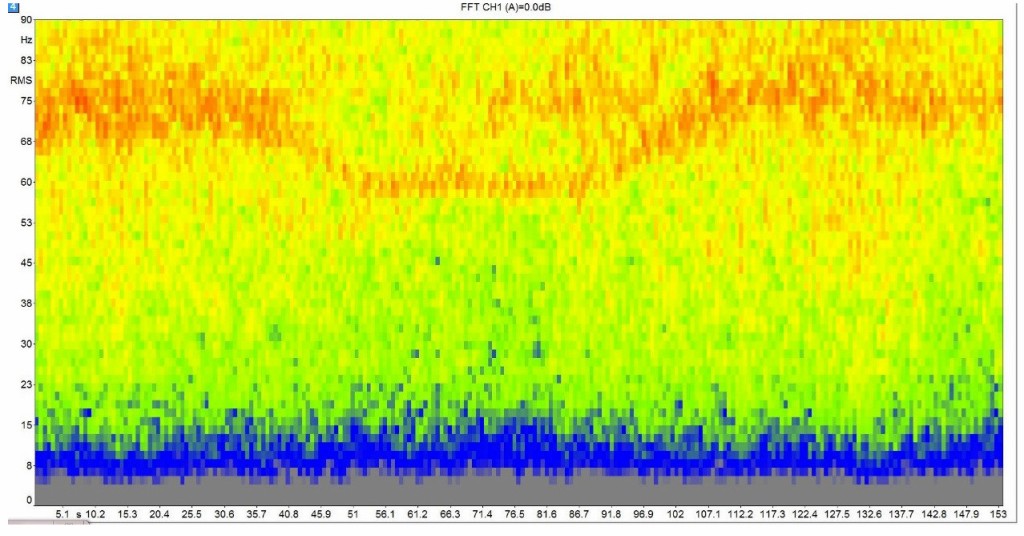
Bild 18 Sonogramm am RMP. Bildausschnitt im Frequenzverlauf bis 90 Hz. Man erkennt eine Art „unscharfen“ Einzelton bei ca. 75-78 Hz. Die WEA verlangsamt sich in der Mitte des Zeitintervalls und die Tonfrequenz verschiebt sich danach auf rd. 60 Hz. Später kehrt die ursprüngliche Tonfrequenz mit unscharfer Breite zurück. Man erkennt – trotz der geringen Zeitauflösung – in der Mitte des Bildes und bei ca. 60 Hz beinahe jede einzelne Rotorblatt-Passage.
Foto: Autor
Bild 18 stellt einen Sonogramm aus einem Messausschnitt von ca. 150 Sekunden Dauer gemessen am RMP dar. Dabei wird in der Darstellung die Frequenz auf den Bereich bis 90 Hz begrenzt. Die Auswertung erfolgte über 12801 Linien des Gesamtsignals, mit Hanning Fenster und exponentieller Mittelung. Die Zeitkonstante betrug 0,32s. Die Zeitauflösung dieser FFT-Analyse ist jedoch 640 ms.
Bei genauerer Betrachtung der Wav- Files ergaben sich (s. [4]) unerwartete Schwierigkeiten. Obwohl die Schallpegelmesser vor Beginn verglichen wurden, fiel es nicht auf, dass der Schallpegelmesser, der als Referenzmikrofon (RMP / R0) diente, bei der Bewertung der Wav auf Z stand und der Schallpegelmesser seitlich (Q) auf A eingestellt war. So ist beim Referenzmikrofon die Messung komplett linear bewertet und die Messung seitlich (Q) in A bewertet. Damit die Ergebnisse repräsentativ miteinander verglichen werden können, wurde bei dem Referenzmikrofon eine nachträgliche A- Bewertung durchgeführt.
Für die näheren Untersuchungen wurden in [4] zehn Zeitpunkte ausgewählt und individuell in der Verstärkung so angepasst, dass sie der Verstärkung im Pegel- Zeit- Diagramm (vgl. [3]) entsprachen. Diese Zeitausschnitte (Zeitpunkte) haben jeweils eine Dauer zwischen zwei und vier Minuten. Diese Zeitausschnitte wurden in [4] mit der Option 1/48 Oktave des Systems Samurai bearbeitet, das eine Frequenzauflösung von 1/48 Oktave (also 16 Teilbänder je Terzband), mit Zeitkonstante FAST (Taktzeit also 125 ms) von 6 Hz bis 20 kHz ermöglicht Diese Daten konnten bei Bedarf jeweils – für die o. a. Zeitabschnitte – komplett numerisch exportiert werden.
Geht man von einer Rotordrehzahl von z. B. U = 13 Umin-1 aus, so beträgt die Winkelgeschwindigkeit der Rotorblätter 1,36 rad s-1. Der Winkelabstand zwischen 2 Rotorblättern beträgt 120 Grad, also 2,094 rad. Somit verstreichen zwischen der Vorbeifahrt zweier Rotorblätter an einem festen Messpunkt, z. B. seitlich der WEA rund 1,54 Sekunden. Bei einer Zeitauflösung des Messsystems von 125 ms ergeben sich etwa 12 Takt-Intervalle, bei denen sich theoretisch ein Einzelblatt dominierend dem Messpunkt annähert und wieder entfernt. Diese Konstellation war bei der gegebenen Drehrichtung der WEA (von vorn gesehen im Uhrzeigersinn) für die beiden neuen Messpunkte ((Q) und Vorn45) gegeben. Für den RMP ist dann die Annäherungsrichtung exakt die abwärts Bewegung mit dem höchsten Wert bei der Passage am Turm. Bei einer Zeitauflösung von 625 ms mit der „normalen“ FFT-Analyse würden nur 3 Intervalle zur Verfügung stehen. Diese Auflösung ist sehr gering. Daher war die Anwendung des Systems 1/48 Oktave in dieser Hinsicht zielführend.
Der Doppler-Effekt bei WEA: Grundlagen
Die Theorie der Geräuschemissionen der WEA unter Berücksichtigung des Doppler-Effektes orientiert sich an zwei Aspekten der Aufgabe. Einerseits die sog. „Retardierung“, d. h. zwischen dem Aussenden des Signals aus der Quelle zum Zeitpunkt t und ihre Ankunft am ruhenden Empfänger zum Zeitpunkt t‘ gibt es eine Zeitdifferenz ∆t = ∆R(t)/c, währenddessen die bewegte Quelle abhängig von ihrer zeitlichen Bewegungscharakteristik sich vom Ort R(t) zu einem anderen Ort R(t‘) begeben hat. Bewegt sich die Quelle nicht, so ist R(t‘) = R(t). D. h. man erhält ein Signal aus einer Quelle mit einer gewissen Zeitverschiebung. Im Mittel über längere Zeiten, die größer sind als ∆t, spielt in diesem Fall die Retardierung eine untergeordnete Rolle. Die relative Bewegung der Quelle zum Messpunkt bewirkt andererseits das Auftreten des sog. Doppler-Faktors, der wie folgt definiert wird.
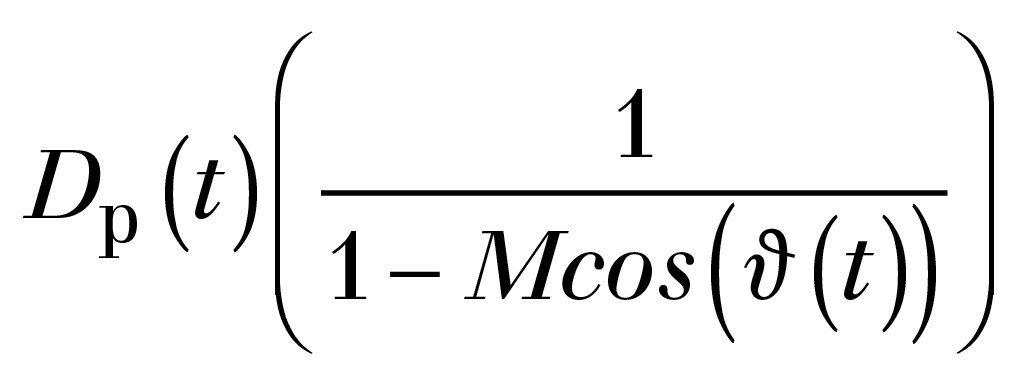 (15)
(15)
Dabei ist M= v/c0 mit der Bezeichnung: M = Machzahl, v = Geschwindigkeit der Quelle und c0 = Schallgeschwindigkeit zu verstehen. Der Winkel V ist der Winkel zwischen dem Vektor der Geschwindigkeit entlang der Bewegung und dem Vektor vom Observer zum Startpunkt der Abstrahlung zur Startzeit t.
Akustisch ist dies ausführlich u. a. von S. Orlemanns in [20] untersucht worden, wobei auch der Fall betrachtet wird, dass zusätzlich zur Bewegung der Quelle auch die Bewegung des Mediums – nicht des Observers – berücksichtigt werden kann.
Eine weitere einfache Darstellung hinsichtlich der Schallabstrahlung einer Punktquelle bei einer linearen Bewegung ist der Arbeit von F. Meng et al. [21] zu entnehmen. Für ausreichende Entfernung zwischen der sich bewegenden Quelle und dem festen Observer gilt bezüglich des Schalldruckes:
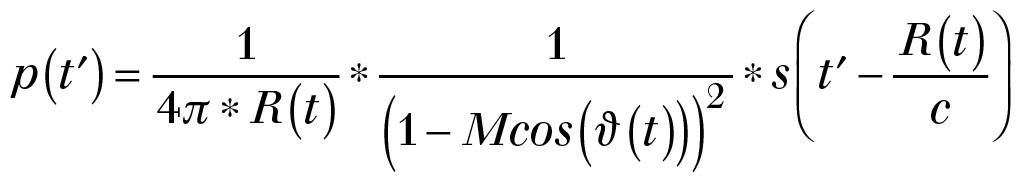 (16)
(16)
Dabei ist s (t) die zeitabhängige Quellencharakteristik. Wenn davon auszugehen ist, dass s(t) = const = S0 also zeitlich konstant ist, kann die Formel vereinfacht werden. Beim Übergang zur Berechnung von Schallpegeln ergibt sich generell:
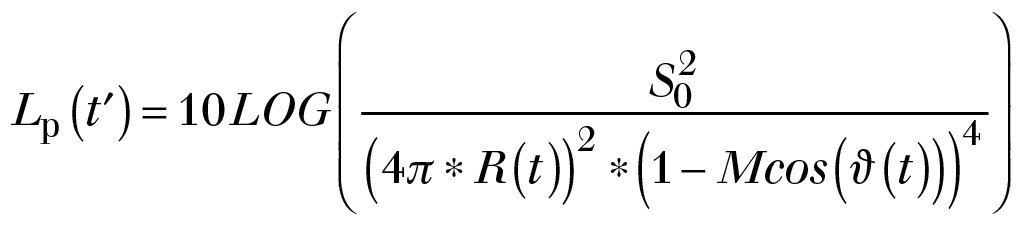 (17)
(17)
Mit anderen Worten, der Doppler-Effekt bewirkt eine zeitliche Verstärkung und Abschwächung der Amplitude abhängig vom Winkel und von der Machzahl.
Der Doppler-Verstärkungsfaktor ist also prinzipiell in der Gl. (15) definiert. Er geht in Gl. 17 mit dem Exponenten (4) ein. Dies wird in [21] angewandt. In den Arbeiten von S. Oerlemanns ([20], [7] WP1) wird darauf hingewiesen, dass der Exponent evtl. höher sein könnte.
Die weitere, mit dem Doppler-Effekt einhergehende Veränderung der Frequenz ergibt sich übrigens aus der Multiplikation der stationären Frequenz mit dem jeweils zutreffenden Wert des Doppler-Faktors nach Gl. (15). Dieser „Frequenz-Sweep“ ist auch Teil der Charakteristik der WEA Geräusche. Das ist hörbar. Es ist schwierig dies bei einer künstlichen Auralisation allein aus den synthetisierten Pegelschwankungen zu simulieren.
Die Größenordnung des Doppler-Verstärkungsfaktors kann näherungsweise mit der Simulation einer Punktquelle an der Blattspitze errechnet werden. Es genügt dabei die Vorgabe der Rotordrehzahl und des Radius. Daraus ergibt sich die Machzahl der Quelle und die Extremwerte ergeben sich aus den extremen Werten von cos(∆)= ±1.
Bei einer Rotordrehzahl von U = 13 Umin-1 und mit Rs = 50 m für die Position der Ersatzpunktquelle ergibt sich eine Tangentialgeschwindigkeit V = 68,07 m/s (ca. 245 km/h). Bei U = 14 Umin-1 ergibt sich entsprechend V = 73,3 m/s (ca. 264 km/h).
Am Messtermin betrug die Lufttemperatur nach eigenen Messungen 9,1 °C im Mittel. Daraus ergibt sich ein Schallgeschwindigkeit von c0 = 336,8 m/s. Hierbei wird die Gleichung
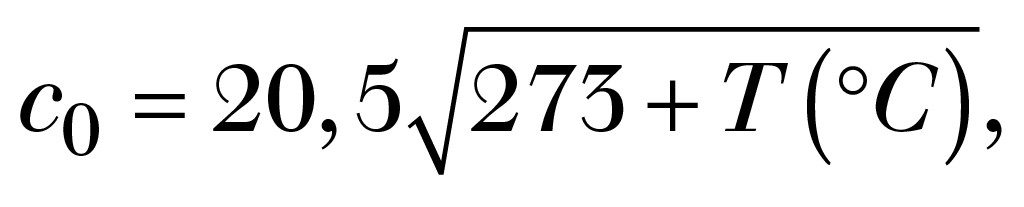 (18)
(18)
verwendet. Die Machzahl M ergibt sich somit zu M = 0,202 bis 0,218 je nach Rotordrehzahl (U=13 Umin–1 bzw. U=14 Umin-1). Bei U=13 Umin-1 beträgt Dp maximal 1,253 also 3,9 dB. Bei U=14 Umin-1 ergibt sich Dp maximal 1,278 also 4,3 dB.
Die o. a. Gleichungen werden im Wesentlichen für lineare Bewegungen angewandt. Im Fall der WEA ist also eine Umrechnung der Schallausbreitung auf die Schallquellen des Rotorblattes durchzuführen. In der Arbeit von B. Zajamsek et al [22] wird ein Modell entwickelt, um entlang des Rotorblattes einzelne Punktquellen zu betrachten, die in Rotation versetzt werden. In diesem Modell wird also explizit die Schallausbreitung von einer Punktquelle im Rotorblatt zum Empfänger betrachtet. Die dazugehörigen geometrischen Daten, wie z. B. Koordinaten des Empfängers, Lage des Rotors, Koordinaten der Ersatzpunktquelle an einer Stelle des Rotors und entlang eines Rotorblattes sind also ortsabhängig (bezüglich der Position entlang des Blattes und während der Rotation des Blattes) berechenbar. In [22] werden dazu diverse Beiträge zur Schallemission und auch Richtwirkungs-Funktionen (vgl. [20] u.a.) betrachtet.
Bezogen auf eine einzelne Schallquelle am Rotorblattende lässt sich eigentlich der Verlauf des Doppler-Faktors während einer Umdrehung einfach berechnen. Allerdings mussten zum Zwecke der Näherungsberechnungen in [4] die Gleichungsansätze in [22], die zu einer Windkanalgeometrie erstellt wurden, auf die realen Koordinaten und Abstände der WEA der eigenen Messungen transformiert werden.
So wurde für die drei Positionen (RMP, Messpunkt seitlich (Q) sowie Messpunkt Vorn 45) des Empfängers und eine Ersatzschallquelle an einer Rotorblattspitze der vermessenen WEA der theoretische Verlauf des Doppler-Faktors einzeln ausgerechnet. Dies erfolgte für eine vollständige Umdrehung in 5 Grad-Schritten. Die Ergebnisse sind in Bild 19 dargestellt.
![Bild 19 Verlauf des Doppler-Faktors für eine Ersatzpunktquelle etwa an der Rotorblattspitze und die vorliegende Messkonfiguration [3],[4] der Messpunkte. Die Variable ist die Winkelposition der Quelle im Koordinatensystem der Rotorebene bei einem festen ‧Radius (s. Text).](https://www.ingenieur.de/wp-content/uploads/2020/12/X754-Bild19.jpg)
Bild 19 Verlauf des Doppler-Faktors für eine Ersatzpunktquelle etwa an der Rotorblattspitze und die vorliegende Messkonfiguration [3],[4] der Messpunkte. Die Variable ist die Winkelposition der Quelle im Koordinatensystem der Rotorebene bei einem festen ‧Radius (s. Text).
Interpretation der Sonogramme im Sinne des Doppler-Effektes
Bei der Auswertung der Sonogramme wurde immer wieder ein tonhaltiges Geräusch festgestellt, mechanischen oder aerodynamischen Ursprungs. Dazu gibt es häufig einen Grundton und einen harmonischen. Eine Auswirkung des Doppler-Effektes ist, dass bei engen Schmalbändern, z. B. mit einer Breite von ca. 1 Hz eine periodische Pegelschwankung um mehrere dB beobachtet werden kann, die bei der gegebenen Zeitauflösung immer noch relativ grob ausfällt.
Werden mehrere Umdrehungen ausgewertet, z. B. über 1 Minute, so erfolgen in solchen Fällen z. B. bei U = 13 Umin-1 insgesamt 3*13 Rotorblatt-Passagen pro Minute am Messpunkt. Insgesamt stehen 480 Werte pro Minute im Schmalband zur Verfügung. Über den relativ periodisch veränderlichen Pegelzeitverlauf kann also am einfachsten eine Pegel-Statistik gebildet werden, wonach sinngemäß die Differenz zwischen Median (50 % Quantil) und z. B. dem 5 % Quantil als ein Maß für die durch den Doppler-Effekt bewirkte Verstärkung berechnet werden kann.
In der Arbeit [4] wurden insgesamt 8 Zeitausschnitte paarweise am RMP oder an den Messpunkten seitlich (SID / Q) bzw. Vorn45° ausgewertet. Dafür wurden folgende Einzelfrequenzen ausgewählt: 59 Hz, 76,6 Hz, 152 Hz, 171 Hz, 505 Hz und 1007 Hz.
Die Auswertungen ergeben ein relativ einheitliches Bild, wonach bei niedrigen Frequenzen die o. a. Differenz stärker ist (mehr als 4 dB) als bei höheren Frequenzen. Das ist in der folgenden Tabelle 3 zusammenfassend dargestellt.
Diese Zusammenhänge bestätigen gewissermaßen die theoretischen Vorstellungen. Weitere Ergebnisse ließen sich auf der Basis der vorhandenen Messdaten im Rahmen einer Ergänzung der Untersuchungen – über die Arbeit [4] hinaus – gewinnen.
Auswertung der Sonogramme zum Doppler-Effekt über einen breiten Frequenzbereich
Zusätzlich zu den vorangegangenen Teil-Auswertungen wurden die Sonogramme vertieft ausgewertet. Darüber wurde ein eigenes Protokoll als Nachtrag zu [4] erstellt. Bei diesen Auswertungen wurde wie folgt vorgegangen:
Export (tabellarisch) der Auswertung von Messdaten in 1/48 Oktave Modus mit 125ms-Takt und Auswahl eines Frequenzbereiches der Auswertung von ca. 25 Hz bis 5 kHz. Die Dauer dieser Zeitfenster betrug in etwa 2 Minuten oder 4 Minuten. Innerhalb dieser Fenster wurden ca. 1 Minute (N = 512 Werte) bzw. ca. 2 Minuten (N = 1024 Werte) einzeln untersucht.
Anstelle der o. a. Perzentil-Methode in [4] wurde die Wavelet-Transformation nach [1] auf die o. a. Zeitreihen des jeweiligen Schmalbandes angewandt, um eine genauere Trendkorrektur auszuführen und somit die Schwankungsbreite des Schmalbandpegels auf diesem Wege alternativ zu bestimmen. Als Kenngrößen wurden in diesem Fall die Werte pAM5o und pAM1o ausgewählt, d. h. die Obergrenze zur jeweiligen Bestimmung nach [1] von pAM5 bzw. pAM1. Damit lässt sich die Verstärkung durch den Doppler-Effekt sehr gut quantitativ beschreiben.
Ergänzend wurde in Schmalbandbreite der Gesamtpegel ermittelt.
Dieses Verfahren wurde auf einem Satz von 9 Zeitreihen am RMP und simultan jeweils am Messpunkt seitlich(SID / Q) oder am Messpunkt Vorn 45° angewandt.
Nachfolgend wird aus diesen Ergebnissen exemplarisch eine Spektrogramm-Serie zu dem Zeitausschnitt Nr. 4 (etwa zwischen 11:32:30 und 11:36:30 Uhr) der Messungen am Referenzmesspunkt (RMP) und praktisch simultan am Messpunkt seitlich (SID/Q) der WEA, die gemäß [3] und [4] vermessen wurde.
Die Zeitauflösung (x-Achse der Sonogramme) beträgt 125 ms, so dass 80-Zeitwerte genau 10 Sekunden sind.Bei der y-Achse der Sonogramme wird die Frequenz in Einheiten von 1/48 Oktavband angegeben. Der Berechnungscode für n in Frequenzen ist: f= exp10 (1,403125 +n*0,00625) ab n = 0 entsprechend 25,3 Hz aufwärts bis 4500 kHz.
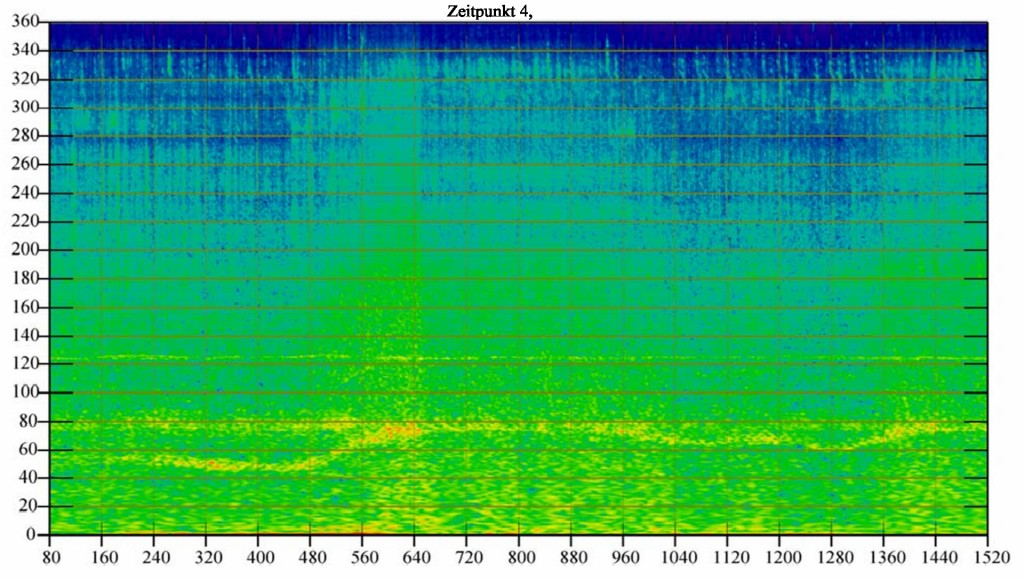
Bild 20 Sonogramm aus den Messungen am RMP (hinten) mit einem variablen Ton zwischen 60 Hz und ca. 75 Hz und einem Oberton bei ca. 150 Hz. Auflösung 1/48 Oktave, Zeitfenster von ca. 3 Minuten Dauer. 10 Sekunden entsprechen 80 Werten.
Foto: Autor
Bild 20 bezieht sich auf die Messung am RMP (hinten).
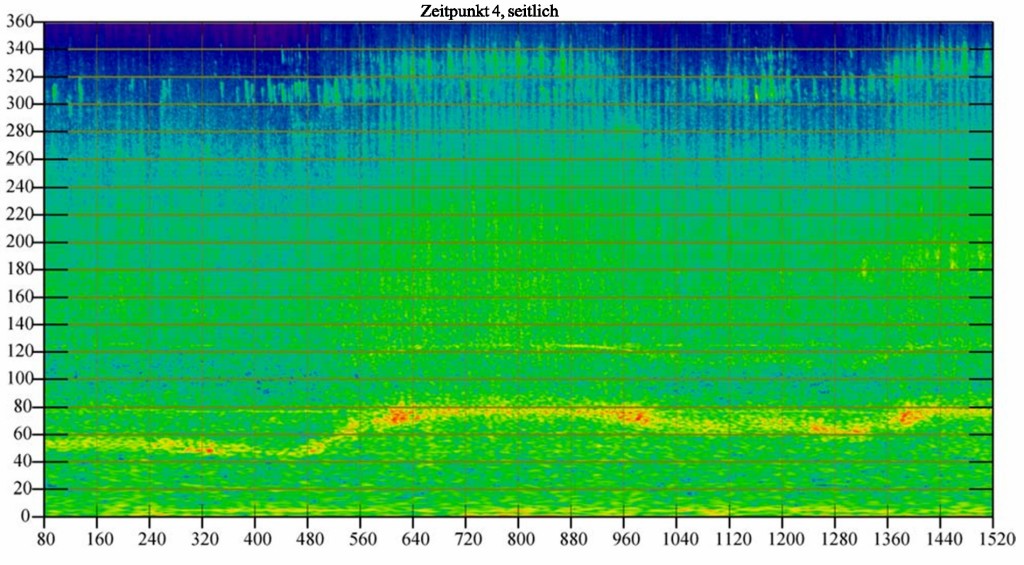
Bild 21 Sonogramm aus den Messungen am Messpunkt SID (seitlich), etwa zeitgleich zu Bild 20 mit einem variablen Ton zwischen 60 Hz und ca. 75 Hz und zeitweise einem Oberton bei ca. 150 Hz. Auflösung 1/48 Oktave, Zeitfenster von ca. 3 Minuten Dauer. 10 Sekunden entsprechen 80 Werten. Bei dieser Abbildung ‧erkennt man leicht AM aber auch die Bewegung der Rotorblätter einzeln am Messpunkt vorbei.
Foto: Autor
Bild 21 stellt die Ergebnisse zeitgleich am Messpunkt SID (seitlich). Aus den Bildern 20 und 21 erkennt man auch im Vergleich deutlich wie die Messdaten nach den Bildern 9 und 10 sich frequenzabhängig prinzipiell entwickeln. Die weiteren nachfolgenden Bilder 22, 23 und 24 stellen die Ergebnisse nach Bild 21 in höherer Zeitauflösung dar.
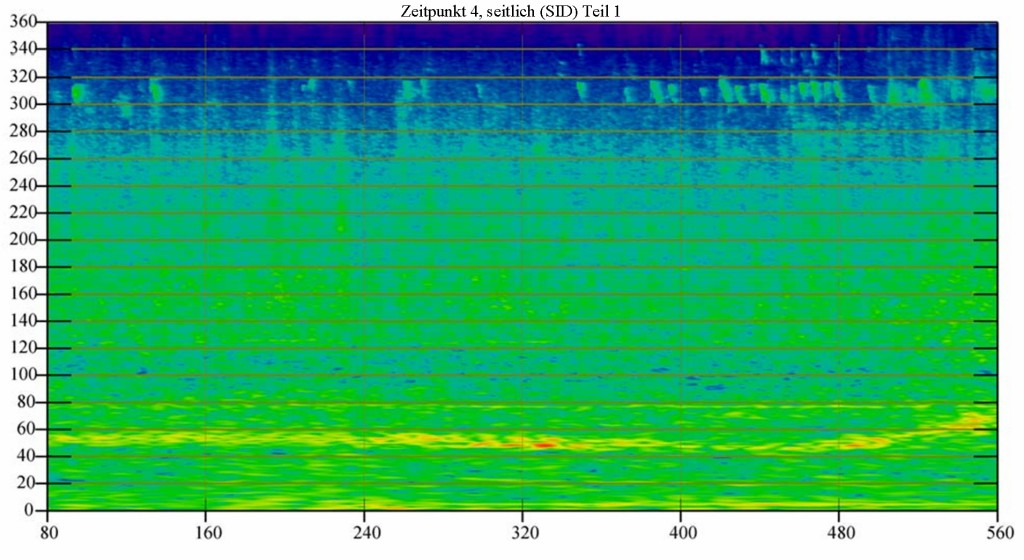
Bild 22 Sonogramm aus den Messungen am Messpunkt SID (seitlich) Teil 1. Die WEA dreht relativ langsam. Der Dauerton bei ca. 52Hz ist immer da. Der Ton bei 78 Hz ist nicht sehr stark. Zum Schluss steigt die Drehzahl.
Foto: Autor
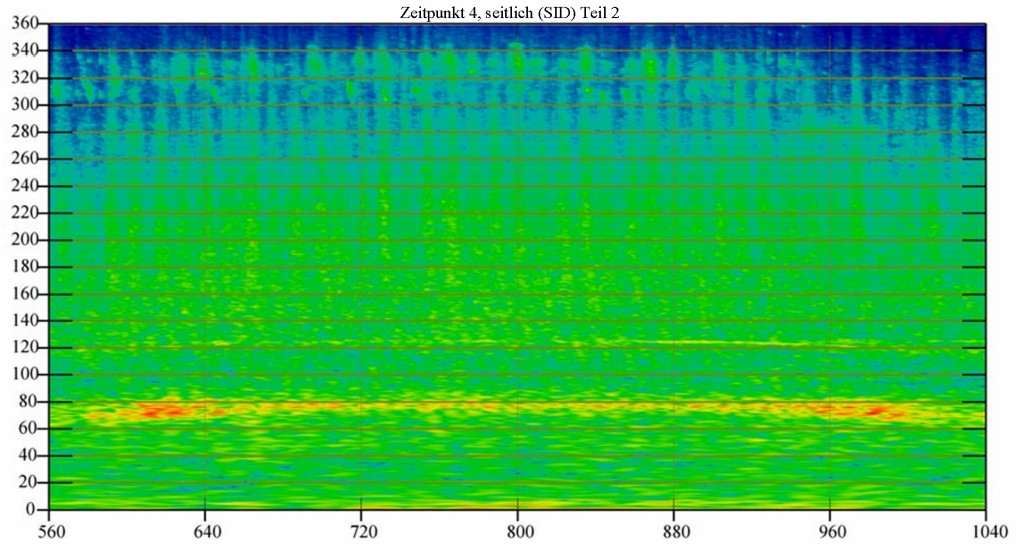
Bild 23 Sonogramm aus der Messung am Messpunkt SID (seitlich), Teil 2. Die WEA dreht sich schneller als bei Teil 1. Der Ton bei 78 Hz ist in dem Mitte des Zeitfensters stabil. Die Verschmierung der Amplitude ist eine Folge des Doppler-Effektes. Zum Schluss nimmt die Drehzahl etwas ab.
Foto: Autor
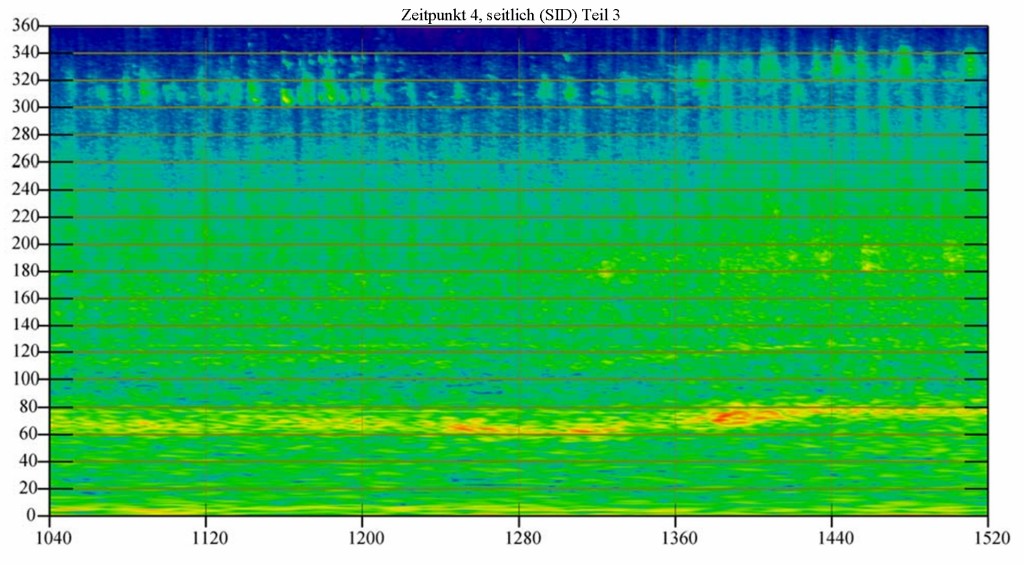
Bild 24 Sonogramm aus der Messung am Messpunkt SID (seitlich), Teil 3. Die WEA dreht sich etwas langsamer als bei Teil 2. Der Ton bei 78 Hz kommt gegen Ende des Zeitfensters wieder. Die Verschmierung der Amplitude in diesem Frequenzbereich ist deutlich eine Folge des Doppler-Effektes. Bemerkenswert sind auch die hochfrequenten Anteile, die auch drehzahlabhängig sind.
Foto: Autor
Die Terzbänder zeigen bei diesen Bilder einen dynamischen Pegelzeitverlauf. Daraus lässt sich das Ausmaß des Doppler-Effektes ermitteln. Um den „Frequenz-sweep“ durch den Doppler-Effekt zu erkennen, muss man eine andere Art der Darstellung wählen.
Sehr deutlich erkennt man auch, dass zeitweise die einzelnen Frequenzbänder gut untereinander korrelieren, zu einem anderen Zeitpunkt aber eben nicht.
![Bild 25 Auswertung im Schmalband des Messzeitraumes 4, Ausschnitt: 128 s Dauer. Messung am RMP hinter der WEA (vgl. [3]).Der Betrag von pAM5o beträgt relativ gleichmäßig ca. 5-6 dB im Bereich bis 200 Hz. Bei höheren Frequenzen bis ca. 2 kHz sinkt es bis knapp 3,5 dB in Übereinstimmung mit der Theorie. Die hohen Werte über 2kHz ergeben sich durch „Singen“ der Rotorblätter in der turbulenten Strömung. Die Einzeltöne, scharf oder unscharf, bei 60 Hz, 75 Hz und 150 Hz sind eindeutig. Der Schalldruckpegel nimmt annähernd linear mit der Frequenz im Bereich von 45 Hz bis 1,5 kHz mit rund 10 dB pro Dekade ab. Quelle: Autor](https://www.ingenieur.de/wp-content/uploads/2020/12/X754-Bild25.jpg)
Bild 25 Auswertung im Schmalband des Messzeitraumes 4, Ausschnitt: 128 s Dauer. Messung am RMP hinter der WEA (vgl. [3]).Der Betrag von pAM5o beträgt relativ gleichmäßig ca. 5-6 dB im Bereich bis 200 Hz. Bei höheren Frequenzen bis ca. 2 kHz sinkt es bis knapp 3,5 dB in Übereinstimmung mit der Theorie. Die hohen Werte über 2kHz ergeben sich durch „Singen“ der Rotorblätter in der turbulenten Strömung. Die Einzeltöne, scharf oder unscharf, bei 60 Hz, 75 Hz und 150 Hz sind eindeutig. Der Schalldruckpegel nimmt annähernd linear mit der Frequenz im Bereich von 45 Hz bis 1,5 kHz mit rund 10 dB pro Dekade ab.
Foto: Autor
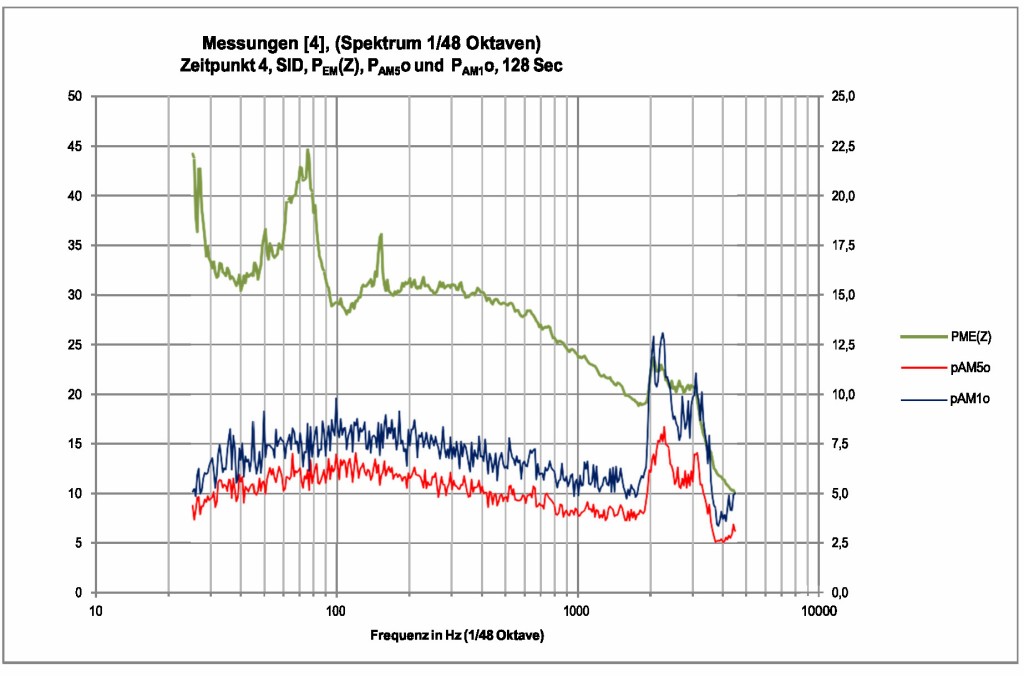
Bild 26 Auswertung im Schmalband des Messzeitraumes 4, Ausschnitt 128 s Dauer. Messungen simultan zu Bild 23 am Messpunkt seitlich (Q, SID). Der Betrag von pAM5o beträgt relativ gleichmäßig ca. 5-6 dB im Bereich bis 400 Hz. Bei höheren Frequenzen bis ca. 2 kHz sinkt es bis knapp 4 dB in Übereinstimmung mit der Theorie. Die hohen Werte über 2kHz ergeben sich durch „Singen“ der Rotorblätter in der turbulenten Strömung. Die Einzeltöne sind ziemlich unscharf bei 60 Hz bis 75 Hz und scharf bei 150 Hz. Der Schalldruckpegel ist annähernd konstant (bis auf den Einzelton bei 150 Hz) im Bereich von 100 Hz bis knapp über 400 Hz, und erst danach nimmt es „linear“ mit dem Logarithmus der Frequenz ab.
Foto: Autor
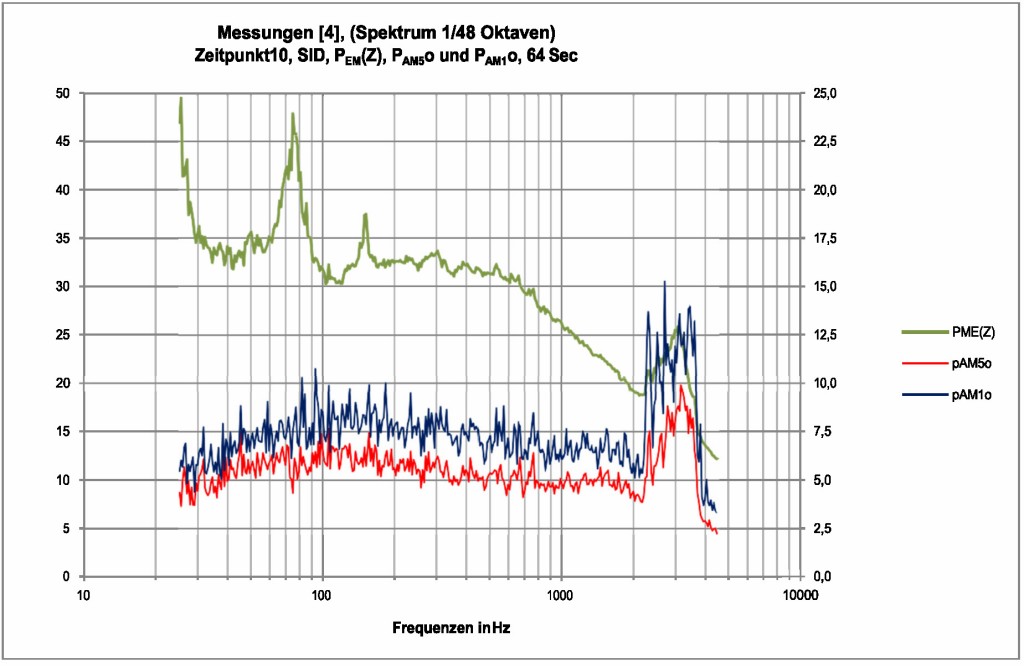
Bild 27 Auswertung im Schmalband des Messzeitraumes 10, Ausschnitt 64 s Dauer. Messungen am Messpunkt seitlich (Q, SID). Der Betrag von pAM5o ist höher als bei Bild 26. Bei höheren Frequenzen bis ca. 2 kHz sinkt es bis knapp 4 dB in Übereinstimmung mit der Theorie. Die hohen Werte über 2kHz ergeben sich durch „Singen“ der Rotorblätter in der turbulenten Strömung, wie bei Bild 24. Die Einzeltöne sind ziemlich scharf bei 75 Hz und bei 150 Hz. Der Schalldruckpegel ist annähernd konstant (bis auf den Einzelton bei 150 Hz) im Bereich von 100 Hz bis knapp über 600 Hz. Bei höheren Frequenzen nimmt es „linear“ bis 2 kHz mit dem Logarithmus der Frequenz ab.
Foto: Autor
Die Bilder 25, 26 und 27 zeigen schließlich eine Verbindung der Schmalbandanalyse mit dem Doppler-Effekt und indirekt mit der Amplitudenmodulation. Die o. a. ausgewiesenen Größen pAM5o und pAM1o sollen nur das Ausmaß des Doppler-Effektes aufzeigen. Die Breite der AM ist mindestens doppelt so groß im Betrag.
Die Bilder 25 und 26 stammen aus simultan erhobenen Messungen. In der Schmalbandanalyse treten also Effekte auf, die bei den üblichen Messungen nach [5] und [6] schwer aufgespürt werden. Auffallend ist, dass in Querrichtung zur WEA (SID,(Q)) die tonhaltigen Komponenten im Spektrum eine ausgesprochene zeitliche Dynamik entwickeln können, sodass die „Töne“ zeitlich verschmiert werden. Dies ist auch in guter Übereinstimmung mit den Daten nach Bild 15 und 17. Die Terzbandkomponenten bei hohen Frequenzen sind allerdings in großer Entfernung u. a. wegen der Luftabsorption nicht wahrnehmbar.
Auch bemerkenswert nach Bild 25 und 26 ist, in Übereinstimmung mit den Messungen an einer E-82 – die im Bericht [23], Bild 3 angegeben werden –, dass in der Querrichtung die Spektren der WEA ein Plateau im mittleren Frequenzbereich aufweisen, das nicht zu der spektralen Charakteristik am RMP passt. Die Arbeit [23] geht auf diesen Befund nicht ein. Die prognostizierten Spektren zur AM von S. Oerlemanns in [7]-WP1 passen auch nicht zu diesem Befund. Auch nicht passend zu dieser Untersuchung und zur Arbeit [3] ist die Theorie der Richtwirkung, die bekanntlich für die Richtung quer zur WEA eine zu starke Pegelabnahme berechnet(z.B. [24]).
Bei Bild 27 handelt sich um eine Messung ebenfalls am Messpunkt SID (seitlich), jedoch zu einem späteren Messzeitpunkt (Nr. 10, 13:01–13:04). Es ergeben sich ähnliche Verhältnisse wie bei Bild 26, allerdings mit stärkerem Doppler-Effekt und mit einer nicht zu breiten Verschmierung der Frequenzen bei rd. 80 Hz.
Ausblick
Es ist einleuchtend, dass der Wirkungsansatz, der entsprechend [2] erörtert wurde, in dieser Form operationell wirksam sein kann, weil es zu einer quantifizierbaren Wirkung von operativen Schallminderungsmaßnahmen führt.
Im Licht dieser Untersuchungen ergibt sich, dass der Doppler-Effekt eine wichtige Rolle bei der Entstehung der AM bei WEA spielt. Die Richtungsabhängigkeit in der Emissionscharakteristik der AM der WEA ist auch z. T. hierin begründet. Die unterschiedlichen Spektren nach Bild 25 und 26/27, in Schmalbandbreite – bereits in Bild 14 und 16 angedeutet – korrelieren nur zum Teil mit dem Befund bezüglich der Kenngrößen pAM5o und pAM1o. Es ist u. E. sinnvoll, ausgehend von diesen Befunden, sowohl künftige wie auch bereits vorliegende Datenbestände mit relevanten Daten einer vertieften Untersuchung zu unterziehen. Das Ziel ist letztlich die Störwirkung der AM durch geeignete Schallminderungsmaßnahmen herabzusetzen.
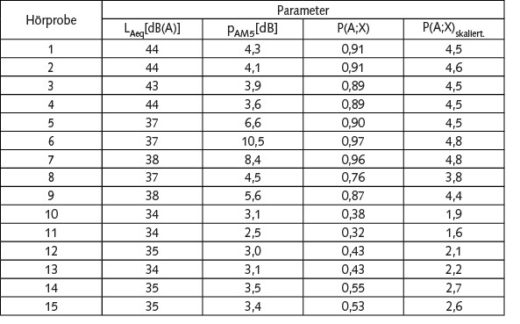
Tabelle 1 Merkmale der 15 Soundfiles.

Tabelle 2 Zeitfenster der analysierten Messdaten.

Tabelle 3 Der Doppler-Effekt bei einzelnen Frequenzen: Differenz Q5%-Q50% (Median) im Zeitintervall in dB. Mittelwerte aus n Messungen.
Literatur:
- Martinez S.; Fennel F.; Pies K.: Amplitudenmodulation als besondere Geräuschcharakteristik der Windenergieanlagen, Lärmbekämpfung 13(2018), Nr. 5, S. 171-182
- Pies K.; Martinez S.; Pies D.: Wirkung der WEA-Geräusche auf Menschen, Fortschritte der Akustik, DAGA 2018, Kiel , S.
- Maleklo A.: Die Richtungsabhängigkeit von Amplitudenmodulation bei Windenergieanlagen, Bachelorarbeit 2019, Technology Arts Sciences TH Köln, Betreuender Professor: Prof. Dr. Christoph Pörschmann ; TÜV Rheinland Energy GmbH
- Ferreira A.-K. R.: Windkraftanlagen und der Doppler-Effekt, Bachelorarbeit 2019, Technische Hochschule Lübeck, 1. Betreuer: Prof. Dr. Jürgen Tschorz; TÜV Rheinland Energy GmbH
- DIN EN 61400–11: Windenergieanlagen-Teil 11: Schallmessverfahren. Berlin: Beuth Verlag 2007.
- Technische Richtlinien für Windenergieanlagen, Teil 1: Bestimmung der Schallemissions- werte, Revision 18. Hrsg: Fördergesellschaft Windenergie e.V. Berlin 2008.
- Renevable UK, Wind Turbine Amplitude Modulation: Research to improve understanding as to its Cause and Effect, December 2013 (WP1 und WP2)
- Janssen, S. A.; Vos H.; Eisses A. R. und Pedersen E.: A comparison between exposure-response relationships for wind turbine annoyance and annoyance due to other noise sources, J. Acoust. Soc. Am. Vol 130, Nr. 6, 2011, S. 3746–3753.
- Pedersen, E.: Health aspects associated with wind turbine noise – Results from three field studies, Noise Control Eng. J. 59, 2011, 47–53.
- Pedersen, E.; Persson Waye, K.: Perception and annoyance due to wind turbine noise – a dose-response relationship, J. Acoust. Soc. Am. (2004). 116, S. 3460-3470
- Bockstael A.; Dekonink L.; Can A.; Oldoni D.: De Coensel B. und Boteldooren D.; Reduction of wind turbine noise annoyance: An operational approach, Acta Acustica united with Acustica, Vol 98(2012) 392-401
- Schäffer B.; Schlittmeier S.J.; Pieren R.; Heutschi K.; Brink M.; Graf R.; Hellbrück J.: Short- term annoyance reactions to stationary and time-varying wind turbine noise and road traffic noise: A laboratory study, J. Acoust.Soc. Am. 139(5) 2016 S. 2949-2963.
- Eggenschwiler K.; Heutschi K.; Schäffer B.; Pieren R.; Bögli H.; Bärtlocher M.: Wirkung und Beurteilung des Lärms von Windenergieanlagen, Aktuelle Beiträge aus der Schweiz, Lärmbekämpfung 11(2016) Nr.5, S. 159–167.
- Pies K.; Daleiden P.; Kemmer F.; Martinez S. C.; Pies D.: Amplitudenmodulation bei Geräuschimmissionen von Windkraftanlagen, Beispiele und Einflussgrößen, Fortschritte der Akustik, DAGA 2018 München, S. 1647-1650
- Kastka J.; Bursch-Galetke E.; Buchta E.; Krauth J.; Mau U.; Muth T.; Schümer R.; Siegmann S.: Untersuchung zum Lärmkontingenzkonzept: Akzeptanz, Belästigungsverhalten und Meinungsbild der Bevölkerung am Beispiel des Düsseldorfer Flughafens 1987–1995, Fortschritte der Akustik, DAGA1996, Bonn
- Lotinga M.; Perkins R.; Singleton R.: Wind Turbine AM Review, Phase 2 Report, Departement of Energy & Climate Change, WSP Parsons Brinkerhoff, August 2016,
- Martinez S.; Fennel F.; Pies K.: Modellierung der Amplitudenmodulation von WEA mit Hilfe eines Drei-Punktquellen-Modells in Anlehnung an IEEE 240, Fortschritte der Akustik, DAGA 2018 München, S. 799-802
- Fukushima, A.; Tachibana, H.: Comparison of the IOA method and Japanese F-S method for quantitative assessment of amplitude modulation of wind turbine noise- A study based on the field measurement results in Japan, Wind Turbine Noise 2017, Rotterdam 2-5. May 2017
- Martinez S.; Fennel F.: Perzentil-Spektren: Merkmalbezogene Kenngrößen bei Geräuschmessungen, Fortschritte der Akustik, Aachen, DAGA 2016, S. 699-702
- Oerlemanns, S.: Detection of aeroacoustic sound sources on aircraft and wind turbines, Thesis University of Twente, Entschede, 2009
- Meng, F.; Behler, G.; Vorländer, M.: A synthesis model for a moving sound source based on beamforming, Acta Acustica u. with Acustica, 104(2018), S. 351-362.
- Zajamsek, B.; Doolan Con, J.; Moreau Danielle, J; Fischer, J.; Prime, Z.: Experimental investigation of trailing edge noise from stationary and rotating airfoils, J. Acoust.Soc. Am. 141(5) 2017 S. 3291-3301.
- Kühner D.: Schallausbreitung von Windenergieanlagen, Akustik Journal 01/19, S. 18-35.
- Lee Seunghoon et al. :Numerical modelling of wind turbine aerodynamic noise in the time domain, J. Acoust. Soc. Am. 133, EL94 (2013).
Dr. Sergio Martinez, Florian Fennel , Anne-Kathrin Ferreira, Ariean Maleklo,
TÜV Rheinland Energy GmbH, Köln.
Kai Pies, Dan Pies,
Schalltechnisches Ing.-Büro Pies GbR, Boppard.

![Bild 8 Windpark am Messtermin aus Sicht der vermessenen WEA [3].](https://www.ingenieur.de/wp-content/uploads/2020/12/X754-Bild8.jpg)










