Qualitätsbestimmung von Immissionsprognosen nach TA Lärm in der Schallschutzpraxis

In der TA Lärm [1] ist es nur eine kleine Randnotiz im Anhang. Bei Schallpegelmessungen sowie detaillierten und überschlägigen Prognosen ist neben einer Vielzahl von Angaben und Informationen im letztendlichen Untersuchungsbericht die Qualität der Messergebnisse/Prognose anzugeben. Was damit gemeint und wie dies zu interpretieren ist, hat in der Vergangenheit zu einem regen Diskurs geführt. Die Grundlagen, mit der eine Unsicherheit einer Messung oder Prognose quantifiziert werden kann, waren in der Vergangenheit bereits das Thema einer Reihe von Veröffentlichungen und Vorträgen, z. B. [2 bis 8], wobei dies in der Regel theoretisch-mathematische Abhandlungen waren. Die Ergebnisse der verschiedenen Autoren decken sich in vielen Teilen, weichen aber im Detail teils deutlich voneinander ab. Einige davon wurden zur Grundlage von Normen, Erlassen und Arbeitsanweisungen, z. B. [9 bis 12].

Dieser Artikel beschäftigt sich im Folgenden ausschließlich mit der Unsicherheit/Qualität von rechnerischen Prognosen, wie sie üblicherweise bei der Genehmigung von (gewerblichen) Anlagen angefertigt werden. Messungen werden hier allenfalls betrachtet, sofern sie zur Bestimmung der Schallleistungspegel einzelner Schallquellen zum Einsatz kommen.

Wie man die größtenteils sehr theoretischen Abhandlungen in der Praxis bei üblichen Immissionsprognosen anwenden kann, versuchte [13] etwas intensiver zu beleuchten. Das Problem dabei ist, dass zwar geeignete Formeln zur Berechnung der Unsicherheit zur Verfügung stehen, die notwendigen Parameter und Eingangsgrößen allerdings nur in den seltensten Fällen. Hinzu kommt, dass die Formeln immer nur bei bestimmten Grundvoraussetzungen gelten, die ebenfalls im Regelfall nicht vorliegen. Der Autor kommt am Schluss zur Erkenntnis: „Forderungen nach einer zahlenmäßig ausgewiesenen Unsicherheit weisen daher in die falsche Richtung. Die Qualität einer Prognose ist dadurch nicht zu beschreiben.“ Grund genug, sich diesem Thema nochmals etwas tiefergehend zu widmen.

Theoretische mathematische Grundlagen

Wenn sich auch die Formeln der genannten Veröffentlichungen im Detail unterscheiden, so gehen sie doch im Wesent­lichen von der gleichen Grundvoraussetzung aus:

• Die Schallleistung jeder einzelnen Schallquelle ist mit einer Unsicherheit behaftet, die durch eine Standardabweichung σ definiert ist. Diese kann wiederum eine Summe verschiedener Unsicherheiten sein. Die Standardabweichung dieser Unsicherheit wird im Folgenden σ_E genannt.
• Die Minderung des Pegels auf dem Schallausbreitungsweg wird nach DIN ISO 9613-2 [14] berechnet, welche wiederum eine Unsicherheit aufweist. Die Standardabweichung dieser Unsicherheit wird im Folgenden σ_D genannt.
• Letztendlich verursacht jede einzelne Schallquelle einen Pegel am Immissionsort, dessen Unsicherheit sowohl von der Unsicherheit der Emission (σ_E) als auch von der der Schallausbreitung (σ_D) abhängt. Die beiden werden dabei als voneinander unabhängig (unkorreliert) betrachtet. Damit lässt sich die Gesamtstandardabweichung einer Quelle am Immissionsort bestimmen. Diese wird im folgenden σ_n genannt.
• Am Immissionsort wirken allerdings in der Regel mehrere Schallquellen ein. Jede für sich ist mit einer Unsicherheit behaftet, die jeweils durch eine Standardabweichung σ_n beschrieben wird. In Abhängigkeit des Pegelwertes (manche Quellen sind dominanter als andere) lässt sich nicht nur der Gesamtpegel am Immissionsort, sondern auch die Gesamtunsicherheit berechnen. Zunächst berechnet man die Gesamtstandardabweichung σ_ges und kann dann mit Hilfe des Erweiterungsfaktors k die zu erwartende Schwankungsbreite für bestimmte Quantile/Perzentile bestimmen. Bei Normalverteilungen gelten folgende Erweiterungsfaktoren (siehe Tabelle 1).

Voraussetzung für die Anwendbarkeit der Berechnungsmethoden

Die zugehörigen Berechnungsformeln sind in den verschiedenen Veröffentlichungen und Normen nachzulesen. Sie sind teilweise ähnlich aber teilweise auch deutlich unterschiedlich. Auffallend ist allerdings, dass alle diese Formeln im Prinzip von identischen Grundannahmen ausgehen, nämlich:

1. Die einzelnen Teilunsicherheiten der Quelle sowie die Gesamtunsicherheit entsprechen einer eingipfligen, symmetrischen Verteilungsfunktion. Eine eingipflige oder unimodale Verteilungsfunktion ist in der Tat sehr häufig zu erwarten. Dies ist zum Beispiel der Fall, wenn man die Emissionen baugleicher Maschinen betrachtet. Aufgrund von Abweichungen bei der Produktion schwanken die Emissionspegel um einen Mittelwert. Wenn die vom Hersteller angegebene Schallleistung dem Mittelwert entspricht, so ist zudem eine symmetrische Verteilungsfunktion zu erwarten. Eine symmetrische, eingipflige Verteilungsfunktion wird „Normalverteilung“ genannt und folgt der entsprechenden Formel (siehe Bild 1).Bei der Anwendung in der Praxis fängt hier bereits das Problem an. Um von dieser Voraussetzung ausgehen zu können, muss der in der Schallprognose verwendete Emissionspegel dem Mittelwert einer solchen Normalverteilung entsprechen und man benötigt die zugehörige Standardabweichung σ_E. Bestimmt man die Schallleistung einer Quelle durch Messungen, so kann man tatsächlich den mittleren Schalleistungspegel ermitteln, benötigt aber für eine verlässliche Aussage eine ausreichende Anzahl von Messungen. Verwendet man, wie in der Praxis üblich, Angaben aus der Literatur oder Fachveröffentlichungen zur Definition der Schallleistung, so sind dies in der Regel Angaben, die die tatsächliche Schallleistung überschätzen. Es sind auf der sicheren Seite liegende Ansätze, die nicht den Mittelwert einer Verteilungsfunktion wiedergeben, sondern irgendwo rechts vom Mittelwert liegen.
2. Die Unsicherheit der Schallausbreitung – im vorliegenden Fall die DIN ISO 9613-2 [14] – entspricht ebenfalls einer symmetrischen Verteilung. Bei tiefergehender Betrachtung unterscheiden sich die verschiedenen Veröffentlichungen allerdings deutlich voneinander. Während die Einen ebenfalls von einer Normalverteilung ausgehen, setzen andere (z. B. die DIN SPEC 45660-2 [9]) eine Rechteckverteilung an.
3. Die einzelnen Teilunsicherheiten sind entweder unabhängig voneinander (unkorreliert) oder es gibt einen kausalen Zusammenhang (korreliert). Korrelierte Unsicherheiten werden teilweise von den Verfassern angesprochen, aufgrund des deutlich höheren Berechnungsaufwands befassen sich die Veröffentlichungen allerdings immer mit dem Sonderfall der unkorrelierten Unsicherheiten.
4. Die Emissionswerte bzw. die prognostizierten Pegel am Immissionsort geben den Mittelwert der zu erwartenden Pegelwerte wieder – ebenfalls eine symmetrische Normalverteilung. Es lässt sich eine Standardabweichung berechnen, mit der sich die Breite bzw. die Perzentile der Verteilung errechnen lassen.

Es ist nun allerdings nicht ausreichend, sich nur für eine der vielen Veröffentlichungen zu entscheiden und diese stur anzuwenden. Viel wichtiger ist die Frage, ob diese Berechnungsverfahren überhaupt im Fall einer konkreten Immissionsprognose anwendbar sind und wenn ja, welche Parameter sind für die Berechnung zu setzen. Es lohnt sich ein tiefergehender Blick auf die einzelnen Aspekte, die maßgeblich die Genauigkeit einer Schallimmissionsprognose bestimmen. Dies sind die Emissionen, das Berechnungsmodell und die Berechnungsrichtlinie.

Unsicherheit der Emission

Die Unsicherheit der Emission einer Schallquelle ist von mehreren Teilunsicherheiten abhängig, z. B.:

Die Unsicherheit der Höhe der Schallleistung

Die verwendete Schallleistung einer Schallquelle ist einer der wichtigsten Faktoren für eine schalltechnische Prognose. Wie bereits erwähnt, wird deshalb im Regelfall auf Ansätze zurückgegriffen, die die tatsächliche Emission etwas überschätzen. Nahezu alle Emissionskenngrößen in der gängigen Literatur liegen auf der sicheren Seite. Sobald diese Ansätze verwendet werden, sind die Berechnungsmethoden zur quantitativen Bestimmung der Gesamtunsicherheit nicht mehr anwendbar. Der Großteil der üblichen Literaturquellen liefert zudem keine Werte für die Standardabweichung der Schallleistung – geht ja auch gar nicht, wenn diese nicht dem Mittelwert entspricht.

Die Unsicherheit im Hinblick auf Dauer und Zeiten der Emission

Auch dies ist einer der wichtigsten Faktoren für das Gesamtergebnis einer schalltechnischen Prognose. Die Frage, wie lange eine Maschine betrieben wird oder wie viele Fahrzeuge einen Parkplatz befahren, ist essenziell für die Höhe des Beurteilungspegels. Auch hier hat sich in der Praxis eingebürgert, dass man nicht von einem (jährlichen) Mittelwert ausgeht, sondern einen exemplarischen Tag mit überdurchschnittlicher Geräuschemission betrachtet. Auch dieser Ansatz „zur sicheren Seite“ lässt eine Berechnung der Gesamtunsicherheit nach den o.g. Methoden nicht mehr zu.

Die Unsicherheit der genauen Lage der Quelle

In vielen Fällen ist die Lage einer Quelle eindeutig bekannt, z. B. der Standort einer Maschine. Allerdings ist bei nicht-ortsfesten Quellen die genaue Lagebestimmung häufig schwierig. Typisches Beispiel ist ein Parkplatz. Bei Supermarktparkplätzen (und natürlich auch anderen Parkplätzen) lässt sich beobachten, dass Besucher gerne nahe des Eingangs parken. Eine gleichmäßige Belegung des Parkplatzes ist nur zu Zeiten hoher Auslastung gegeben. Wie genau sich der Parkverkehr über den Parkplatz verteilt, ist von Tag zu Tag und Stunde zu Stunde unterschiedlich und lässt sich in der Regel auch nicht eindeutig ermitteln. Der Ersteller der Schallimmissionsprognose macht in diesen Fällen etwas, das er in solchen Fällen immer macht. Er trifft einen Ansatz zur sicheren Seite, d. h. er bildet nicht mehr den Mittelwert ab. Und schon sind die o. g. Berechnungsmethoden auch bezüglich dieses Aspekts nicht mehr anwendbar. Das macht aber nichts, denn für die Standardabweichung hätte er ohnehin keinen Wert zur Verfügung gehabt.

Die Unsicherheit der Richtwirkung bzw. Abstrahlcharakteristik

Jede Schallquelle hat eine Richtwirkung, d. h. die von ihr emittierte Schallenergie wird ungleichmäßig in den Raum abgegeben. Allgemein üblich ist es aber, nur die Gesamtschallleistung einer Quelle anzugeben. So machen es Hersteller von Maschinen und so ist es in der Regel auch bei Emissionsangaben in der Literatur. Es ist hier durchaus mit richtungsabhängigen Schwankungen von bis zu 10 dB(A) oder noch mehr zu rechnen.

Kommunikationsfehler

In der Abstimmung zwischen Gutachter und Auftraggeber oder beim Verwenden von Literaturquellen ist es durchaus möglich, dass es zu Verständnis- oder Kommunikationsfehlern kommt, die sich letztendlich in einer unzutreffenden Emissionsangabe darstellen können. Die DIN SPEC 45660-1 erwähnt als einzige der vielen Veröffentlichungen diesen Aspekt, sagt aber, dass er kaum quantifizierbar ist und daher am besten ignoriert werden sollte.

Ein sorgfältiges Vorgehen und die Berufserfahrung des Gutachters helfen, diesen Fehler zu vermeiden oder zumindest sehr gering zu halten.

Unsicherheit der Berechnungsrichtlinie

Die wellenförmige Schallausbreitung in drei Raumdimensionen ist mathematisch schwer zu fassen. Im Freifeld kommt man noch zu einer vergleichsweise einfachen Lösung einer Linearkombination von ebenen Wellen in die einzelnen Raumrichtungen. Sobald aber noch Beugung, Streuung oder zeitliche Interferenzen hinzukommen, gerät man selbst mit heutigen Rechenprozessoren schnell an die Grenzen des Machbaren. Daher wird die Schallausbreitung normalerweise mit Näherungsverfahren berechnet, z. B. mit dem Strahlverfolgungsverfahren (Raytracing) oder der Schallteilchenmethode (Sound Particle Diffraction). Die DIN ISO 9613-2 verwendet das Strahlverfolgungsverfahren und geht davon aus, dass die Quelle „Schallstrahlen“ in alle Richtungen aussendet. Je nachdem, was dem Strahl auf dem Weg zum Immissionsort alles widerfährt, bestimmt sich der Geräuschpegel am Immissionsort. Mathematisch wird dies durch verschiedene Minuenden A ausgedrückt, die die Minderung auf dem Ausbreitungsweg aufgrund der verschiedenen Einflüsse abbilden. Diese wurden teils analytisch (Abstandsminderung A_div), größtenteils aber empirisch (z.B. Abschirmung A_bar) ermittelt. Eine solche hilfsweise Nachbildung der tatsächlichen Schallausbreitung ist logischerweise mit einer gewissen Unsicherheit behaftet. Zum Beispiel liefert die DIN ISO 9613–2 im Grenzbereich der Abschirmung (also wenn der Schallstrahl knapp über ein Hindernis hinweg geht bzw. gerade so unterbrochen wird) einen unsteten Übergang. Es kommt zu einem Pegelsprung, der in der Realität nicht festgestellt werden kann. Besondere Schwierigkeiten hat die Richtlinie auch bei kleineren Durchgängen oder Schlitzen. Es wird hier die Beugung grundsätzlich nur über die Abschirmungskante und nicht über die Größe der Öffnung bestimmt. Dennoch macht die ISO 9613-2 unter Ziffer 9 eine Aussage zu ihrer Genauigkeit (siehe Tabelle 2).

Doch selbst wenn man diese Hürden meistern würde und zu einer Standardabweichung für die Schallausbreitung gelangt, so wäre dieser Wert dennoch aus folgenden Gründen nur sehr eingeschränkt für die Berechnung der Ausbreitungsunsicherheit tauglich:

• Er gilt nur im Bereich des angegebenen Abstands und der mittleren Höhe (dies ist in der Regel noch erfüllt).
• Er gilt nur für Situationen ohne Reflexion und Abschirmung. Übliche Umgebungsverhältnisse beinhalten normalerweise immer reflektierende und abschirmende Objekte. Außerdem bleibt so die Problematik der teils realitätsfremden Abbildung von Beugungskanten unbeachtet.
• Bei besonders tieffrequenten Geräuschen, bei denen die Wellenlänge ähnliche Größenordnungen erreicht wie die Hindernisse auf dem Ausbreitungsweg, liefert das Schallstrahlverfahren grundsätzlich unzuverlässige Ergebnisse. Daher ist in der DIN ISO 9613-2 auch eine untere Grenzfrequenz von 63 Hz vorgesehen.
• Das von der DIN ISO 9613-2 vorgegebene Verfahren zur Bestimmung der maßgebenden Schallwege ist kein volldrei­dimensionales Verfahren, sondern nur quasidreidimensional (getrennte Suchen in horizontaler und vertikaler Ebene). Bei ungünstigen räumlichen Anordnungen werden ggf. wichtige Schallwege nicht berücksichtigt.
• Die DIN ISO 9613-2 bildet einen zeitlichen Mittelwert der Ausbreitungsbedingungen ab. Die Pegel am Immissionsort können bei größeren Abständen zur Schallquelle aufgrund lokaler Verhältnisse innerhalb von Sekunden stark schwanken. Dies ist u. a. einer der Gründe, warum die DIN ISO 9613-2 bei der Prognose von einzelnen Geräuschimpulsen (z.B. Schießlärm) nicht angewendet werden sollte.

Unsicherheit des verwendeten Rechenmodells

Schalltechnische Prognosen werden in der Regel mit einem speziell dafür vorgesehenen Berechnungsprogramm durchgeführt, in dem zunächst eine dreidimensionale Rekonstruktion der tatsächlichen Verhältnisse stattfindet. Dorthinein werden dann die Schallquellen positioniert. Die Schallausbreitungsberechnung wird von diesen Programmen durchgeführt, die die entsprechenden Berechnungsrichtlinien (im vorliegenden Fall die DIN ISO 9613-2) implementiert haben. Alle gängigen Berechnungsprogramme haben die Rechenrichtlinien „korrekt“ implementiert, was sich dadurch nachweisen lässt, dass die entsprechenden Beispielaufgaben der Richtlinie im Rahmen der geforderten Genauigkeit gelöst werden. Allerdings bilden diese Beispielaufgaben zumeist sehr simple geometrische Situationen ab. Bei komplexen Geometrien ist es durchaus zu erwarten, dass die Berechnungsprogramme unterschiedliche Berechnungsergebnisse liefern können.

Mit zunehmendem Detailgrad des Rechenmodells verbessert sich die Genauigkeit in Bezug auf die reale Situation vor Ort, allerdings nur bis zu einem gewissen Grad. Ab dem Erreichen einer gewissen Genauigkeitsstufe der Modellbildung erhöht sich nur noch die Berechnungsdauer ohne Verbesserung der Ergebnisse. Bei zu detailreichem Rechenmodell kann sogar eine Umkehrbewegung stattfinden, bei der die Ergebnisse wieder realitätsferner werden. Meistens hat dies mit zu fein aufgeteilten Reflexionsflächen zu tun, die dann die Größenordnung der Wellenlängen erreichen. Auf diese Weise liefert die DIN ISO 9613-2 nicht nur im tieffrequenten, sondern sogar bis in den mittelfrequenten Bereich hinein ungenaue Ergebnisse. Allgemeingültige Empfehlungen zum sinnvollen Detailgrad eines Rechenmodells gibt es nicht. Es ist immer von der Situation im Einzelfall und dem Fingerspitzengefühl des Gutachters abhängig. Eine zahlenmäßige Quantifizierung dieses Unsicherheitsfaktors ist normalerweise unmöglich.

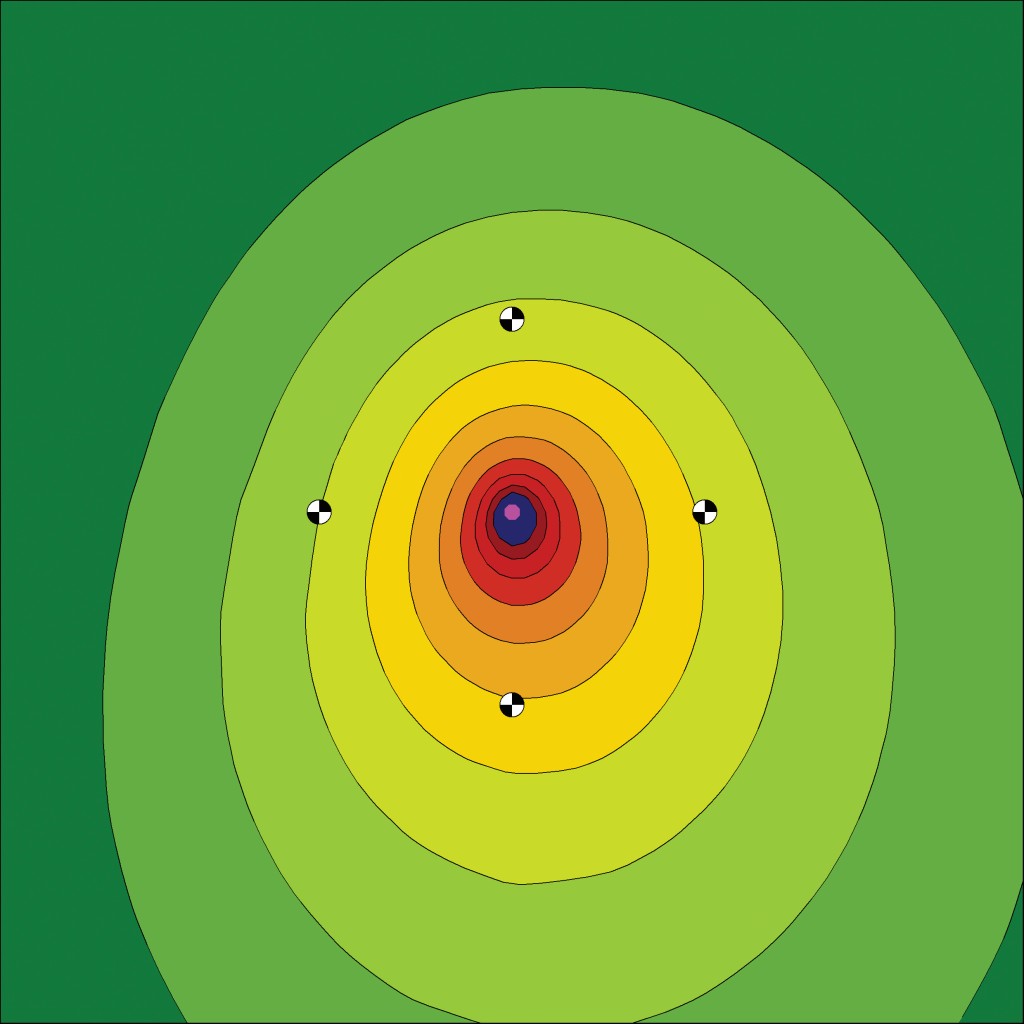
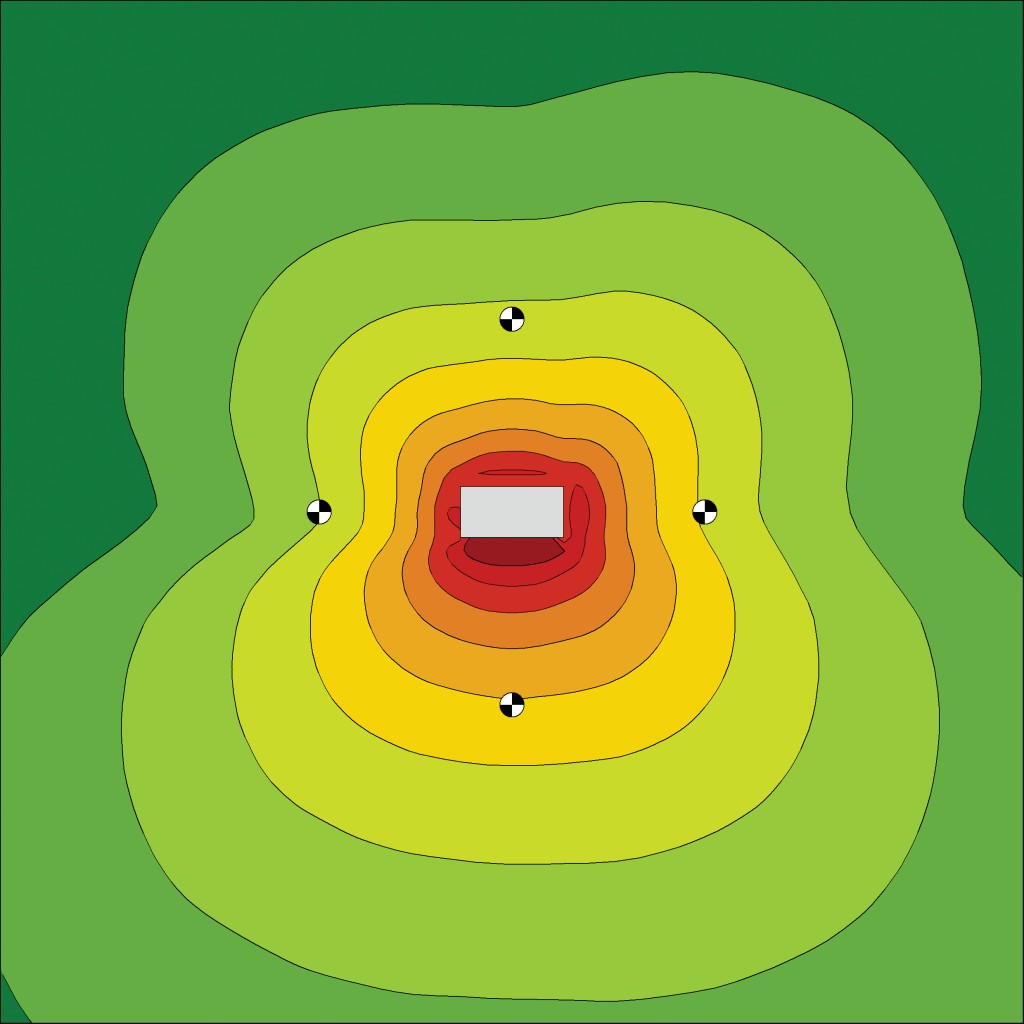
Selbst wenn genaue Angaben zur Emission einer Quelle vorliegen, z. B. gemessene Pegel rings um eine Maschine, spielt es eine entscheidende Rolle, wie man diese Quelle im Rechenmodell nachbildet. Dies zeigt folgendes Beispiel, bei dem eine Maschine mit ringsum bekannten Schalldruckpegeln einmal als punktförmige Schallquelle mit Richtwirkung und einmal als abstrahlender Quader abgebildet wurde. Trotz identischer Pegelwerte an den vier Messpunkten ergeben sich dennoch deutlich unterschiedliche Schallabstrahlcharakteristiken (siehe Bild 2 und 3).

Jede Teilquelle verursacht am Immissionsort einen Pegel, dessen Unsicherheit von den o. g. jeweiligen Einzelunsicherheiten der Emission, des Rechenmodells und der Rechenrichtlinie abhängt. Wie beschrieben, ist es im Regelfall nicht möglich, diese Einzelunsicherheiten zu quantifizieren.

Durch Addition der Teilpegel wird am Schluss der Gesamt­beurteilungspegel am Immissionsort gebildet. Hätte man belastbare Informationen über die jeweiligen Einzelunsicherheiten, könnte man die Gesamtunsicherheit des Ergebnisses berechnen, z. B. nach dem Fehlerfortpflanzungsgesetz, wenn alle Unsicherheiten voneinander stochastisch unabhängig wären.

Leider ist dies in der Realität eigentlich nie der Fall. Es gibt Unsicherheiten, die unmittelbar miteinander korrelieren, z. B. die Anzahl der Parkbewegungen auf einem Supermarktparkplatz und die Anzahl der Einstapelvorgänge der Einkaufswagen am Einkaufswagensammelpunkt. Solche vollständig korrelierten Unsicherheiten ließen sich – wenn auch mit etwas erhöhtem Aufwand – berücksichtigen.

Ganz kompliziert und nahezu nicht mehr berechenbar wird es, wenn zwischen den Unsicherheiten Teilkorrelationen bestehen. Dies kann zum Beispiel die Emission betreffen. Ein Jumbo-Sattelzug fasst 34 Europaletten. Bei einer täglichen Anlieferung von 1 bis 34 Paletten ist also grundsätzlich nur ein Lkw notwendig. Die Schallquelle „Lkw-Fahrbewegung“ ist unabhängig von der Quelle „Entladen Paletten mit Gabelstapler“. Wenn nun aber mehr als 34 Paletten geliefert werden, ist ein zweiter Lkw notwendig – und damit liegt eine teilweise oder nicht lineare Korrelation vor.

Darüber hinaus ist es so, dass zwar häufig die Schallquellen untereinander unkorreliert sind, die Ausbreitungsbedingungen aber korreliert. Auf dem Betriebsgrundstück nahe beieinanderliegende Schallquellen haben nahezu die identischen Schallausbreitungsbedingungen zum Immissionsort. Hier lässt sich das Fehlerfortpflanzungsgesetz nicht anwenden.

Fazit

Es gibt mathematische Methoden zur quantitativen Bestimmung der Unsicherheit einer schalltechnischen Prognose. Diese sind allerdings nur in einem relativ schmalen Bereich anwendbar. Alle Quellen und Schallausbreitungsbedingungen müssen statistisch voneinander unabhängig sein, es müssen belastbare Erkenntnisse über die Unsicherheit der einzelnen Quellen vorliegen und es müssen vergleichsweise einfache Schallausbreitungsbedingungen ohne Abschirmung und Reflexionen vorliegen. Windenergieanlagen sind beispielsweise (zumindest näherungsweise) für eine derartige Unsicherheitsbestimmung geeignet.

Beim überwiegenden Anteil schalltechnischer Prognosen lässt sich die Unsicherheit quantitativ nicht angeben. Dies ist immer dann der Fall,

• wenn es keine Angaben über die Standardabweichung der jeweiligen Quellen gibt. Die gibt es in den wenigsten der allgemein üblichen Literaturquellen, bei Ermittlung der Emission durch eigene Messungen lässt sie sich nur mit einem sehr hohen Aufwand (große Anzahl an Messungen) bestimmen.
• wenn die Quellemissionen oder das Betriebsszenario „zur sicheren Seite hin“ abgeschätzt werden. Dies ist in nahezu allen Literaturangaben und schalltechnischen Prognosen der Fall.
• wenn die Teilpegel der einzelnen Quellen am Immissionsort weder vollständig korreliert noch vollständig unabhängig voneinander sind. Auch dies ist in der Praxis in sehr vielen Fällen zutreffend.
• wenn auf dem Weg des Schalls von der Quelle zum Empfänger die Reflexion oder Beugung eine relevante Rolle spielt.

Ein Versuch, die Unsicherheit dennoch über mathematische Vereinfachungen und frei abgeschätzte Parameter zu bestimmen, kann keine sinnvollen Ergebnisse liefern. Die Beliebigkeit der Vorgehensweise ermöglicht es, jedweden gewünschten Wert zu errechnen.

Andere Methoden zur Bestimmung der Gesamtunsicherheit einer Schallimmissionsprognose, z. B. empirisch durch nachträgliche Messung an zuvor durch Prognose vorhergesagten Situationen, bieten sich leider ebenfalls nicht an. Da das angesetzte Betriebs- und Emissionsszenario in der Regel die tatsächlichen Verhältnisse überschätzt, ist durch Messung weder eine Validierung der Prognose noch eine Bestimmung der Unsicherheit möglich. Außerdem setzt die DIN ISO 9613-2 bei der Ausbreitungsberechnung grundsätzlich eine leichte Mitwindsituation an. Bei einer Messung können andere Windverhältnisse herrschen.

Die Erkenntnis aus [13], dass die Qualität einer Prognose nicht durch eine zahlenmäßig ausgewiesene Unsicherheit beschrieben werden kann, wird damit bis auf wenige Ausnahmefälle (z.B. Windenergieanlagen) bestätigt.

Bei genauerem Hinsehen stellt man auch fest, dass in der TA Lärm keine Aussage zur Unsicherheit (quantitativ), sondern eine Aussage zur Qualität (qualitativ) gefordert wird. In den Auslegungshinweisen zur TA Lärm [15,16] wird nochmals klargestellt, dass die TA Lärm keinen quantitativen Toleranzbereich festlegt. Vielmehr ist, wenn die Beurteilungspegel nahe den zulässigen Immissionsrichtwerten liegen, auf eine hohe Genauigkeit in Hinblick auf Betrachtungstiefe und Detailschärfe zu legen. Ist eine deutliche Einhaltung oder Überschreitung der Anforderungen ohnehin absehbar, darf das Berechnungsmodell auch gerne etwas gröber ausfallen.

Es sollte im Bericht zur schalltechnischen Prognose dargelegt werden, auf welcher Datengrundlage die Prognose erstellt wurde, an welcher Stelle und in welcher Weise der Gutachter mit den Ansätzen zur sicheren Seite gegangen ist und wie er selbst die Ergebnisse einschätzt. Gerade die fachgutachterliche Einschätzung, die auf einer fundierten Basis aus physikalischem, juristischem und lärmmedizinischem Wissen beruht, ist in den vergangenen Jahren häufig hinter einer rein verwaltungsrechtlichen Betrachtungsweise verloren gegangen.

Literatur

[1]  TA Lärm (Technische Anleitung zum Schutz gegen Lärm): 6. allg. Verw.v. zum Bundes-Immissionsschutzgesetz vom 28. August 1998, zul. geänd. durch die Bekanntm. des BMUB vom 1. Juni 2017 (BAnz. AT 08.06.2017 B5).

[2]  Martinez, S.C.: Qualität von Immissionsprognosen nach TA Lärm, Lärmbekämpfung 47 Nr. 2, März 2000.

[3]  Martinez, S.C.: Angabe der Messunsicherheit bei Prognosen nach TA Lärm: Aufwand und Ergebnis in der Praxis, DAGA 2005.

[4]  Kurze, U.: Abschätzung der Unsicherheit von Immissionsprognosen, Lärmbekämpfung 48 (2001) Nr. 5.

[5]  Probst, W.; Donner, U.: Die Unsicherheit des Beurteilungspegels bei der Immissionsprognose, Lärmbekämpfung 49 Nr. 3, Mai 2002.

[6]  Probst, W.: Berechnung der Unsicherheit bei Immissionsprognosen nach TA Lärm, April 2009.

[7]  Geissler, P.; Gilg, J.: The Importance of Human Factors for the Uncertainity of Environmental Noise Prediction of Industrial Plants, Symposium „Managing Uncertainity in Noise Measurement and Prediction“ Le Mans, 27-29 Juni 2005

[8]  Heiss, A.; Krapf, K.-G.: Quantification of uncertainity by real time confidence limits in separation of sound immission levels, Noise Control Eng. 55(1), Jan/Feb 2007

[9]  DIN SPEC 45660-1: Leitfaden zum Umgang mit der Unsicherheit in der Akustik und Schwingungstechnik – Teil 1: Unsicherheit akustischer Kenngrößen, Berlin: Beuth Verlag 2014.

[10]  Erlass des Ministeriums für Landwirtschaft, Umweltschutz und Raumordnung des Landes Brandenburg zu Anforderungen an die Geräuschimmissionsprognose und an die Nachweismessung bei Windenergieanlagen (WEA) – (WEA-Geräuschimmissionserlass) vom 31. Juli 2003

[11]  Einige Handreichungen zu Fragen der Statistik, Wahrscheinlichkeit und Genauigkeit für die Anwendung im Immissionsschutz vor Geräuschen, Landesumweltamt NRW, Mai 2003

[12]  Zum Nachweis der Einhaltung der Immissionswerte mittels Prognose, Erfahrungsaustausch mit den Meß- und Prüfdiensten „Geräusche und Erschütterungen“ im LUA, Landesumweltamt NRW, 2001.

[13]  Danner J.: Qualität von Schallimmissionsprognosen bei Industrieanlagen, VGB PowerTech 5/2007

[14] DIN EN ISO 9613-2: Dämpfung des Schalls bei der Ausbreitung im Freien, Teil 2: Allgemeines Berechnungsverfahren, Berlin: Beuth Verlag 1997.

[15]  Auslegungshinweise zur TA Lärm 98, Vorschriftensammlung der Gewerbeaufsicht Baden-Württemberg, Version 03/2003.

[16]  LAI-Hinweise zur Auslegung der TA Lärm in der Fassung des Beschlusses zu TOP 9.4 der 133. LAI-Sitzung am 22. und 23. März 2017.

[17]  VDI-Richtlinie 3723: Anwendung statistischer Methoden bei der Kennzeichnung schwankender Geräuschimmissionen, Berlin: Beuth Verlag 1993.