RMS ist das Maß für thermische Belastung

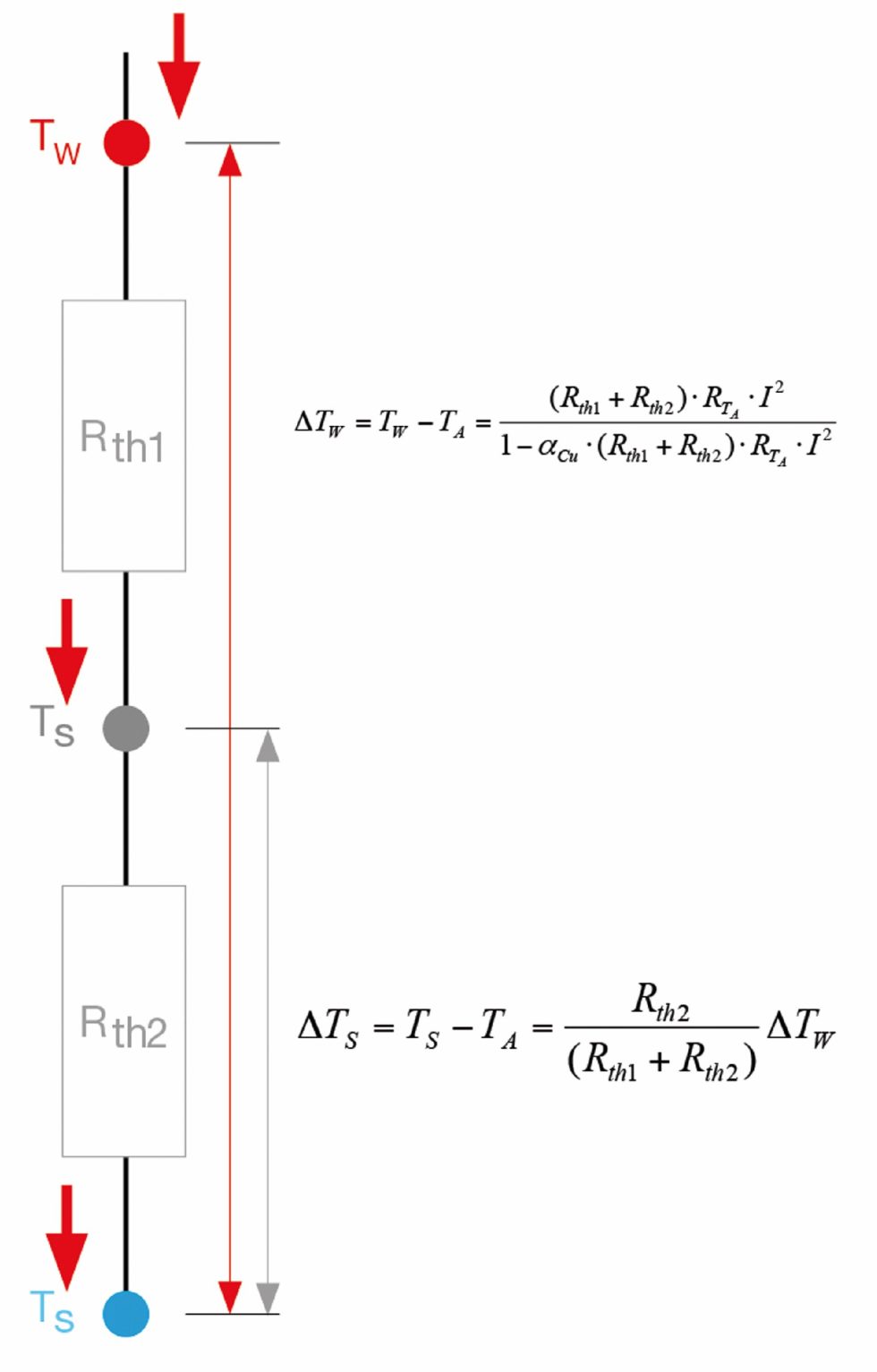
Bild 1 Abschätzung der Erhöhung von Wicklungs- (TW) und Gehäusetemperatur (TS) im Dauerbetrieb (ohne Berücksichtigung der Erwärmung durch Wirbelstromverluste) in Bezug auf die aktuelle Umgebungstemperatur (TA). Rth1: thermischer Widerstand Wicklung – Gehäuse; Rth2: thermischer Widerstand Gehäuse – Umgebung (kann von Montagebedingungen beeinflusst werden); RTA: der elektrische Anschlusswiderstand bei aktueller Umgebungstemperatur; I: die Strombelastung; aCU: Temperaturkoeffizient des elektr. Widerstands von Kupfer (ca. 0,004 K-1). Der Nenner in der ersten Formel berücksichtigt die Temperaturabhängigkeit des elektrischen Widerstands. In Gleichung 2 agieren die thermischen Widerstände als „Spannungsteiler“ für die Temperatur. Bild: maxon

Wie heiß wird ein Motor im Betrieb? Solche Temperatur- abschätzungen sind im Dauerbetrieb bei konstanter Last einfach zu realisieren. Nach genügend langer Zeit stellt sich ein thermisches Gleichgewicht ein, das mit Hilfe der ther-mischen Widerstände des Motors R_th1 und R_th2 berechnet werden kann (Bild 1). Zuerst wird die Erwärmung der Wicklung aus der Joule’schen Verlustleistung in der Wicklung berechnet, anschließend die Erwärmung des Motors als Ganzes (des Stators).

Belastung bei zyklischem Betrieb

Wie sehen die Berechnungen von Bild 1 für zyklischen Betrieb aus, mit einer Abfolge von unterschiedlichen Strombelastungen? Wird der Arbeitszyklus inklusive kurzer Pausen viele Male wiederholt? Wird sich mit der Zeit ein ther- misches Gleichgewicht einstellen? Aber wo liegt es?

Zur Berechnung der thermischen Belastung zieht man den Effektivwert des Stroms oder des Drehmoments bei. Dies ist ein quadratischer Mittelwert, der die überproportionale Erwärmung bei hoher Belastung berücksichtigt und von der Stromrichtung unabhängig ist. Im Eng- lischen wird diese Mittelung als RMS (Root Mean Square) bezeichnet, was eine perfekte Anleitung für die Berechnung ist: Man nehme die Wurzel aus dem zeitlichen Mittel der aufsummierten quadratischen Belastungen. Als Formel sieht dies beispielsweise für den Strom wie folgt aus:

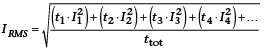
Dieser RMS-Stromwert wird in die Formel für die Erwärmung der Wicklung in Bild 1 eingesetzt. Analog könnte man auch die Drehmomente mitteln.

Beispiel: Erwärmung eines Motors im Handgerät

Ein sterilisierbarer Motor ECX Speed 22 L (36-V-Wicklung) soll in ein medizinisches Handgerät eingebaut werden. Während der 10 Zyklen soll die Temperatur um nicht mehr als 20 °C ansteigen. Da das Gerät direkt in der Hand des Arztes liegt, darf die Außenhülle nicht wärmer als 40 °C werden. Die Belastungsangaben zum Betriebszyklus : siehe Bild 2.

Können die thermischen Vorgaben erfüllt werden?

Dazu zuerst einmal ein paar Überlegungen zu den Belastungsdauern. Ein Zyklus inklusive Pausen dauert fast 3 Minuten, 10 Zyklen praktisch eine halbe Stunde. Der Motor hat eine thermische Zeitkonstante von etwas über 8 Minuten, sodass am Ende der 10 Zyklen das thermische Gleichgewicht praktisch erreicht wird. Somit können wir im Sinne einer Worst-Case- Betrachtung die Berechnungen für die Gleichgewichtstemperatur anwenden. Dies ist zusätzlich gerechtfertigt, da uns nur die Gehäusetemperatur interessiert, welche nur träge mit der schon erwähnten Zeitkonstante reagiert. Die längste Belastungsphase ist mit 1 Minute nur ein Bruchteil davon, sodass die Temperaturabweichungen am Gehäuse nur sehr gering sind.

Zu den geforderten Drehmomenten gilt es festzustellen, dass alle Werte bedeutend kleiner sind als das Nenn­moment des Motors von etwa 33 mNm. Der Motor wird also nur schwach belastet, und es ist mit einer kleinen Erwärmung zu rechnen. Die Drehzahl ist nur in den ersten 15 Sekunden wirklich hoch, sodass wir die Erwärmung durch Wirbelströme vernachlässigen können.

Lassen wir den Motor mit dem vorgegebenen Belastungszyklus laufen, so ist dies aus thermischer Sicht äquivalent mit einem Dauerbetrieb mit dem Effektivwert oder RMS-Wert der Belastung. Einsetzen der Drehmomente in die Berechnungsformel ergibt:

Der Motor hat eine Drehmomentkonstante von 6,11 mNm/A, sodass sich eine effektive Strombelastung von: I = 16,3 mNm / 6,11 mNm / A = 2,67 A ergibt.

Setzt man dies in die Gleichung zur Erwärmung der Wicklung in Bild 1, ergibt das 15 Kelvin. Das Gehäuse erwärmt sich im Verhältnis der thermischen Widerstände etwas weniger, nämlich um ca. 14 Kelvin. Bei 20 °C Umgebungstemperatur resultiert somit eine Gehäusetemperatur von knapp unter 35 °C. Beide Werte, Erwärmung als auch Endtemperatur, liegen innerhalb der zulässigen Grenzen. Dies gilt auch, wenn man die Temperaturvariationen innerhalb eines Arbeitszyklus von grob abgeschätzten +/- 3 Kelvin berücksichtigt.