Theoretische und experimentelle Ermittlung der O-Ring-Berührbreite
Zur Ermittlung der Berührbreite von O-Ringen werden oftmals Finite-Element-Berechnungen durchgeführt, mit denen das Dichtungsverhalten bei der Montage, im Betrieb sowie unter auftretenden Temperatur- und Druckbelastungen simuliert werden kann. Gerade im Stadium der Vorauslegung würde es jedoch oftmals schon genügen, eine schnelle Abschätzung vornehmen zu können. Dieser Beitrag gibt einen kurzen Überblick über verschiedene in der Literatur beschriebene Verfahren zur Ermittlung der O-Ring-Berührbreite. Ein Versuchsaufbau zur Untersuchung der Geometrie verpresster Dichtungen wird beschrieben und eine neue Methode zur Ermittlung der O-Ring-Berührbreite vorgeschlagen. Die verschiedenen Verfahren werden anhand der Messwerte und der Ergebnisse anderer Autoren vergleichend gegenübergestellt.
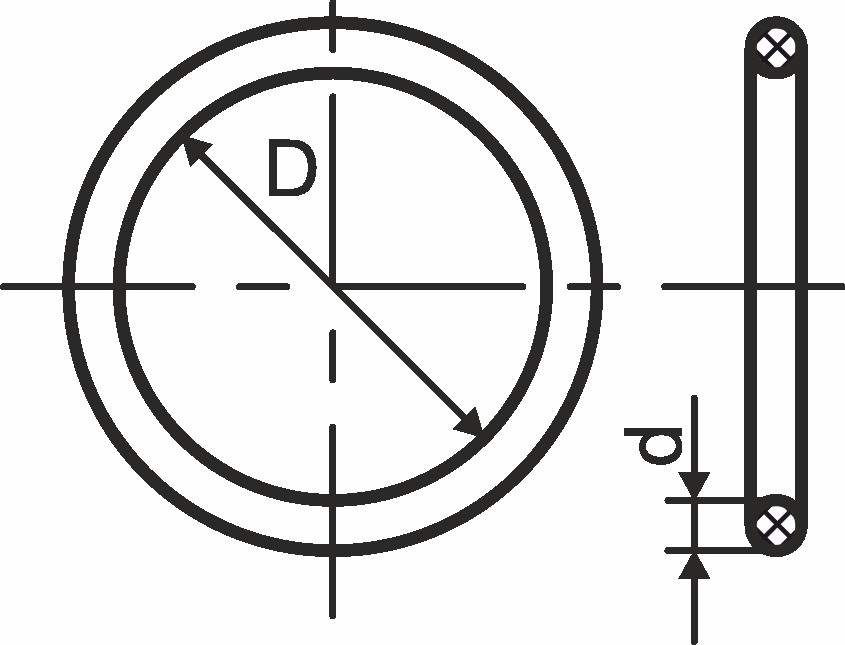
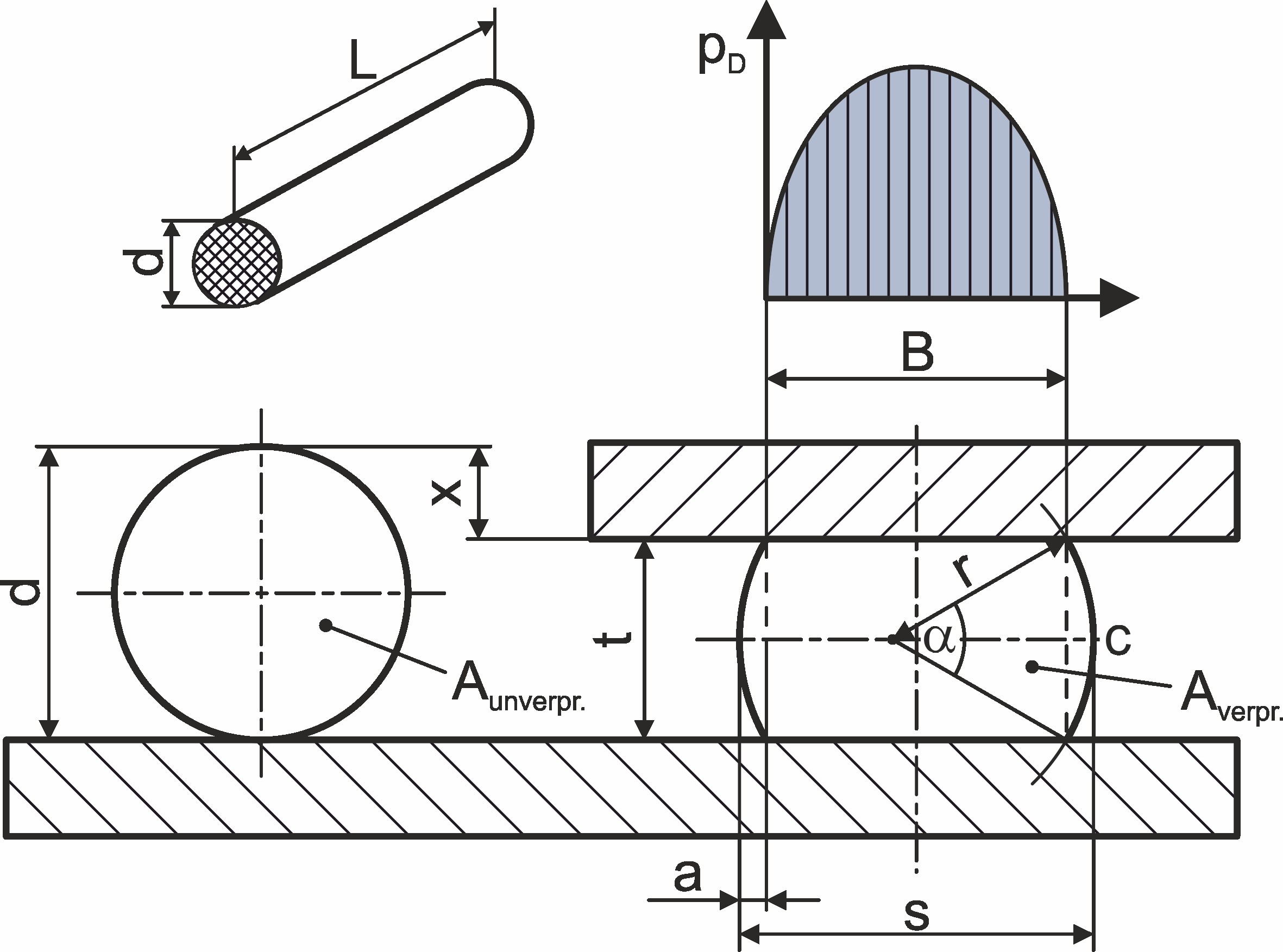
Bild 1 Geometrie eines O-Rings. Bild: Verfasser
Einleitung
Der O-Ring ist aufgrund seiner einfachen Form und seiner guten Verfügbarkeit in den verschiedensten Abmessungen und Werkstoffen die weltweit wohl am häufigsten eingesetzte Dichtung. Er lässt sich durch seinen Innendurchmesser D und seinen Schnurdurchmesser d beschreiben, s. Bild 1. Die Dichtwirkung eines O-Rings basiert auf dem Bestreben des elastomeren Dichtungsmaterials, nach einer Deformierung in seine ursprüngliche Form zurückzukehren. Durch eine radiale oder axiale Verpressung des O-Rings bei der Montage bildet sich daher im Kontaktbereich zwischen Dichtfläche und Elastomerdichtung die zur Abdichtung notwendige Dichtpressung pD aus, Bild 2.
Im drucklosen Zustand ist diese Pressungsverteilung ungefähr parabelförmig. Ein anliegender Druck überlagert sich diesem Verlauf aufgrund der automatischen Dichtwirkung des elastomeren O-Rings [1]. Damit ist das Maximum der Flächenpressung immer größer als der abzudichtende Druck.
Entscheidend für die Höhe und den Verlauf der Dichtpressung ist auch die Berührbreite B, an der die Dichtung an der Dichtfläche anliegt. Besonders bei Dichtsystemen, die in korrosiven Umgebungen eingesetzt werden, stellt die Berührbreite ein entscheidendes Auslegungskriterium dar. Bei statischen Gehäusedichtstellen kann unter korrosiver Belastung das Fehlerbild der korrosiven Dichtungsunterwanderung auftreten [2]. Über Berührbreite und Dichtpressung lässt sich die Unterwanderungsbeständigkeit des O-Rings bewerten [3].
Um eine Dichtstelle unter diesen Gesichtspunkten zuverlässig auslegen zu können, ist es daher unabdingbar, die Größe der Berührbreite schon während der Konstruktion zu kennen.
In der Literatur beschriebene Verfahren
Je nach Einbausituation eines O-Rings kann es nach der Montage zu einer Anlage der Dichtung an einer oder beiden Nutwänden kommen. Entsprechend können daher, wie in Bild 3 dargestellt, drei Fälle unterschieden werden: die seitlich unbehinderte, einseitig oder beidseitig behinderte Ausdehnung.
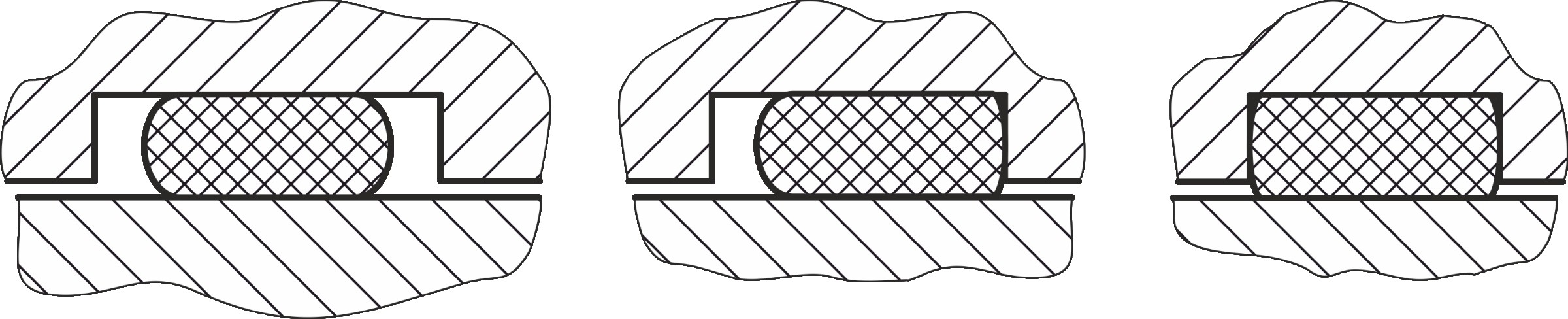
Bild 3 Unbehinderte (l.), einseitig (m.) und beidseitig (r.) behinderte Einbausituation. Bild: Verfasser
Die Verformung des Dichtungsprofils, und damit auch die Größe der Berührbreite, ist entsprechend vom Einbau abhängig. Die nachfol- genden Ausführungen beziehen sich auf den Fall der seitlich unbehinderten Ausdehnung im drucklosen Zustand.
Die Einbausituation eines verpressten O-Rings wird üblicherweise als Hertz’scher Kontakt angesehen. Wenn die Abmaße des O-Rings deutlich größer sind als die der Kontaktzone, kann von einem ebenen Dehnungszustand ausgegangen werden [4]. Der Verlauf der Flächenpressung über der Berührbreite nimmt hierbei die Form einer Parabel an und entspricht der bekannten Herzt‘schen Pressung [5]. Unter diesen Annahmen leitete Lindley für den Fall einer unbehinderten seitlichen Ausdehnung den in Gl. (1) angegebenen Zusammenhang ab [6], [7]. Der erste Term entstammt hierbei der Hertz’schen Theorie, wohingegen der zweite Term empirisch ermittelt wurde, um eine Korrektur für hohe Verpressungsgrade vorzunehmen [8].
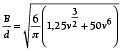 (1)
(1)
Gl. (1) gibt die auf den Schnurdurchmesser d normierte Berührbreite B als Funktion von der Verpressung v an. Hierbei ist:
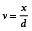 (2)
(2)
Der Verpressweg x berechnet sich aus der Höhe der verformten Dichtung t und dem Schnurdurchmesser d entsprechend Gl. (3):
x = d – t (3)
Bei der Herleitung von Gl. (1) wurden folgende Annahmen getroffen:
– Die Elastizitätsmoduln der abzudichtenden Gehäuse sind unendlich, verglichen mit dem Elastizitätsmodul des elastomeren O-Rings.
– Das Dichtungsmaterial ist inkompressibel (Querkontraktionszahl µ = 0,5).
Diese Überlegungen verstoßen allerdings gegen einige Voraussetzungen der Hertz’schen Theorie, bzw. sind für O-Ringe nicht ausreichend nachgewiesen. Dennoch zeigen Vergleiche, dass diese Methode bis zu Verpressungsgraden von 25 % oder 30 % ohne wesentliche Fehler angewandt werden kann [5], [9].
Eine ebenfalls von Lindley vorgeschlagene experimentelle Formel zur Ermittlung der Berührbreite ist in Gl. (4) angegeben [10]:
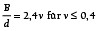 (4)
(4)
Für seitlich unbehindert eingebaute O-Ringe ermittelte Wendt experimentell den in Gl. (5) angegebenen Zusammenhang [8], [10].
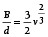 (5)
(5)
Gl. (6) stellt eine von Gorelik und Feld’man vorgeschlagene Methode dar, die auf den Schnurdurchmesser normierte Berührbreite in Abhängigkeit von der Verpressung zu ermitteln. Dieser Ansatz ist mit der von Jagger und Walker vorgeschlagenen Formel identisch [10].
(6a)
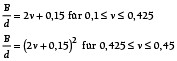 (6b)
(6b)
Karaszkiewicz formulierte ebenfalls einen empirischen Vorschlag zur Ermittlung der Berührbreite eines verpressten O-Rings, s. Gl. (7) [11].
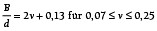 (7)
(7)
Ebenso ermittelte er die in Gl. (8) angegebene Formel zur Berechnung der Breite s der verpressten Dichtung [11]:
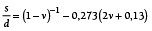 (8)
(8)
Durch Approximation experimenteller Ergebnisse leiten Dragoni und Strozzi hierfür den folgenden Zusammenhang ab [12]:
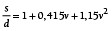 (9)
(9)
Die Anwendbarkeit der genannten Ansätze wurde verschiedentlich untersucht und mit Messungen und Finite-Element-Simulationen ver-glichen [7], [8], [10]. Insbesondere bei Verpressungen größer 20 % variiert ihre Aussagefähigkeit.
Experimentelle Ermittlung der O-Ring-Berührbreite
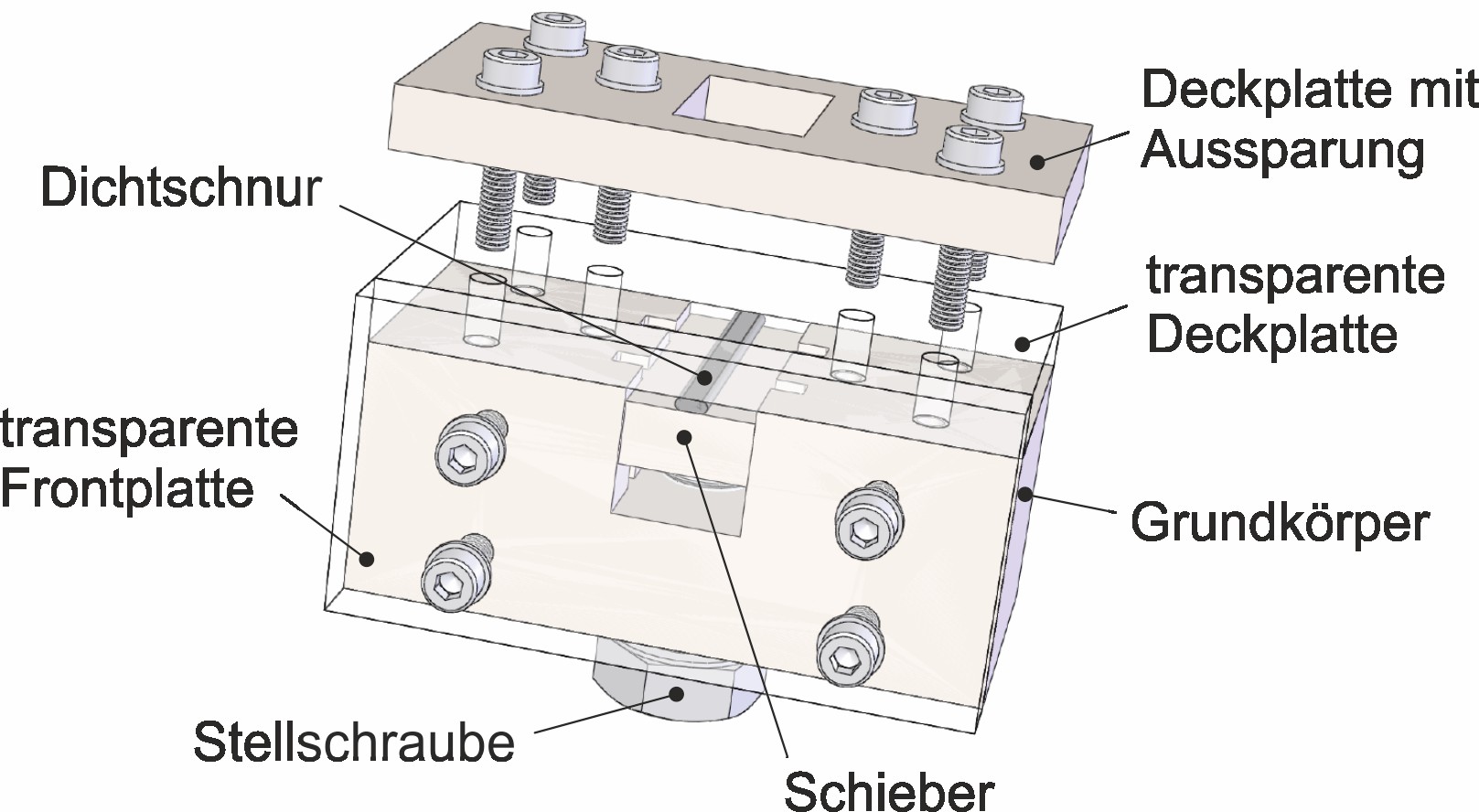
Für einen Vergleich der Aussagefähigkeit der verschiedenen Verfahren wurden die Berührbreiten von runden Dichtschnüren bei unterschiedlichen Verpressungen gemessen. Hierzu wurde der in Bild 4 dargestellte Aufbau entwickelt.
Er besteht aus einem quaderförmigen Grundkörper, in dessen Nut ein Schieber aus Acrylglas über eine Stellschraube bewegt werden kann. Um ein Verkippen zu verhindern, läuft er seitlich in je zwei Führungsnuten. Die Dichtschnur wird über diesen Schieber gegen die transparente Deckplatte aus Acrylglas verpresst. Zur Er-höhung der Steifigkeit wird eine zusätzliche Deckplatte aus Aluminium angebracht. Eine Aussparung in dieser Platte ermöglicht den Blick von oben auf die verpresste Elastomerdichtung. Durch die geradlinige Ausrichtung der runden Dichtschnur kommt es im Vergleich zur ringförmigen Anordnung zu Abweichungen im Verformungsverhalten. Dies dürfte allerdings nur bei sehr kleinem Innendurchmesser D relevant sein. Dafür bietet sich die Möglichkeit, den verformten Profilquerschnitt zu betrachten. An ihren Stirnflächen würde sich die Dichtschnur aufgrund der ungehinderten Ausdehnungsmöglichkeit in axialer Richtung anders verformen. Um dies zu verhindern, liegt die Elastomerdichtung an einer transparenten Frontplatte aus Acrylglas an.
Dieser Aufbau ermöglicht es, die Geometrie der Dichtung bei variabel einstellbaren Verpressungsgraden unter dem Lichtmikroskop zu betrachten und zu vermessen. Bild 5 zeigt Mikroskopaufnahmen eines verpressten O-Rings. Das linke Bild wurde durch die transparente Frontplatte aufgenommen. Hier kann der Radius r des Kreissegments sowie die Höhe t des verformten O-Rings gemessen werden. Über die Dichtungshöhe t lässt sich mit den Gln. (2) und (3) die Verpressung berechnen. Bild 5 rechts zeigt eine durch die transparente Deckplatte gemachte Aufnahme. Sie dient zur Ermittlung der Berührbreite B und der verpressten Dichtungsbreite s.
Bei der Vermessung des verformten O-Ring-Querschnitts durch die transparente Frontplatte wurde festgestellt, dass sich die gemessenen Berührbreiten an den beiden Dichtflächen mitunter deutlich unterscheiden, vgl. Bild 5 links. Ursache hierfür ist die während des Verpressens auftretende Reibung zwischen Elastomerdichtung und Frontplatte. Allerdings tritt dieser Effekt nur unmittelbar an der Stirnseite auf. Die durch die obere Deckplatte gemessenen Werte für die Berührbreite B werden dadurch nicht beeinflusst. Dies wurde mit pressungsempfindlichen Messfolien überprüft. Hierzu wurde jeweils eine Folie zwischen den Dichtflächen und der Dichtschnur platziert. Unter dem Druck des verpressten Elastomers platzen in die Folie integrierte Mikrofarbkapseln auf und führen zu einer Rotfärbung. Auf diese Weise kann die Berührbreite an den Pressungsabdrücken gemessen werden. In ausreichendem Abstand von der Stirnfläche der Dichtschnur unterscheiden sich die Ergebnisse zwischen oberer und unterer Dichtfläche nicht mehr. Durch die Reibung zwischen Frontplatte und Elastomerdichtung kann es auch zu geringen Unregelmäßigkeiten des Radius r kommen. Diese betreffen allerdings nur einen kleinen Bereich im Übergang zur Berührbreite und können vernachlässigt werden. Der Radius r wird als Mittelwert aus den gemessenen Radien der linken und rechten Seite des Dichtungsquerschnitts bestimmt.
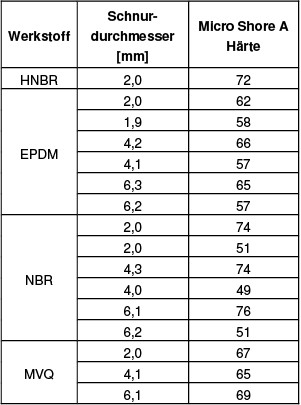
Eine Übersicht der verwendeten Elastomerdichtungen zeigt Tabelle 1.
Um herstellungsbedingte Einflüsse der Dichtungen auszuschließen, wurden Proben aus jeweils einer Charge verwendet. Mit jeder dieser Dichtschnüre wurden bei Raumtemperatur mehrere Messungen mit unterschiedlichen Verpressungen durchgeführt.
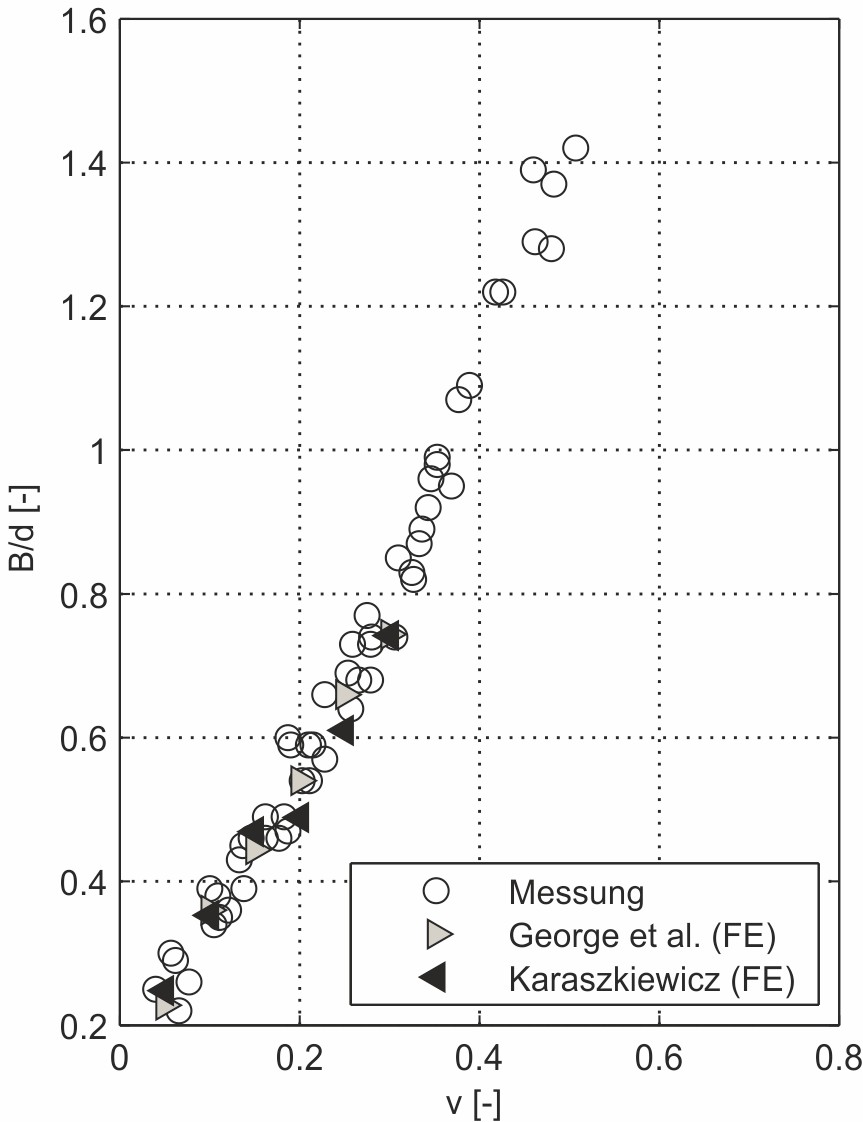
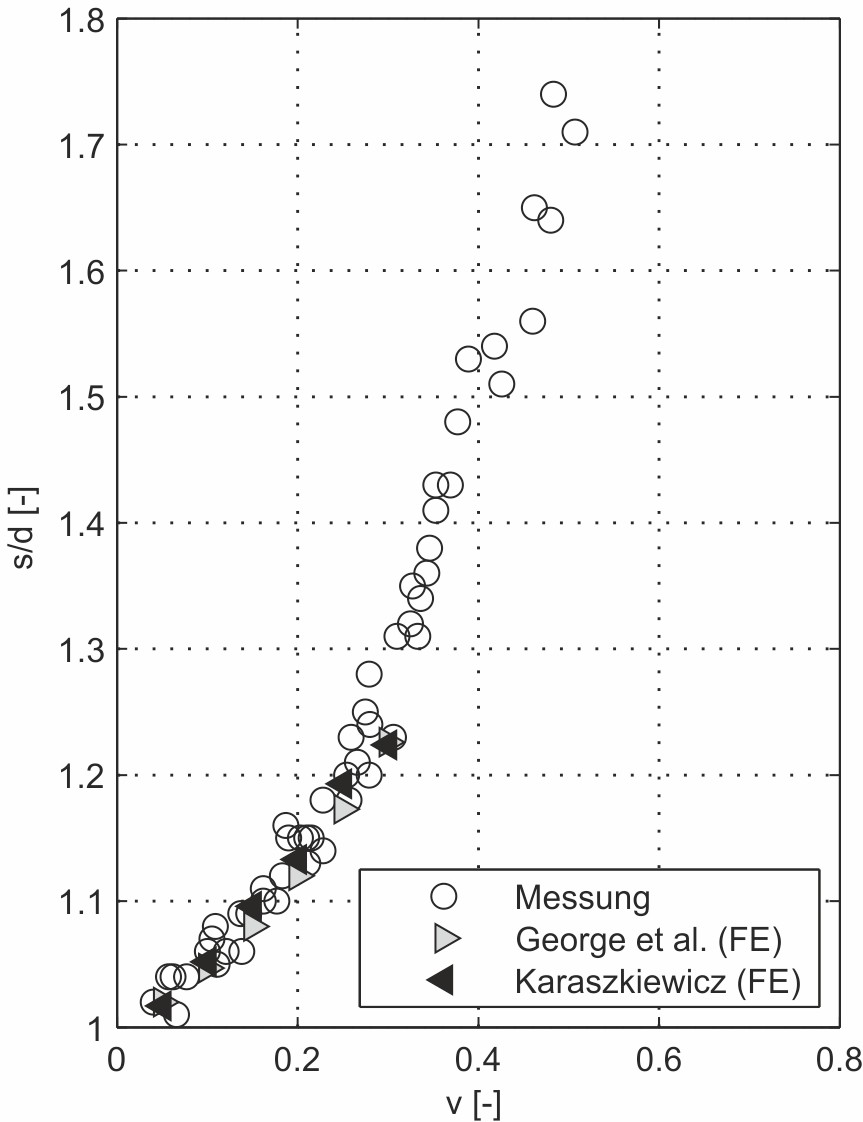
Die Messwerte sind in Bild 6 bis Bild 8 auf den Schnurdurchmesser normiert dargestellt.
Darüber hinaus sind die Ergebnisse der Finite Element (FE)- Berechnungen von Karaszkiewicz [11] und George et al. [11], [14] für die Berühr- und Dichtungsbreite eingetragen. Die Messdaten liegen in sehr guter Übereinstimmung mit diesen FE-Berechnungen.
Methode basierend auf inkompressiblem Werkstoffverhalten
Elastomere O-Ringe können aufgrund ihres annähernd inkompressiblen Verhaltens (Querkontraktionszahl µ ≈ 0,5) wie hochviskose Flüssigkeiten mit sehr hohen Oberflächenspannungen betrachtet werden [13]. Unter Annahme einer Volumenkonstanz der Dichtung im unverformten und verformten Zustand lässt sich folgender Zusammenhang formulieren, wenn davon ausgegangen wird, dass sich die Dichtungslänge L beim Verpressen des O-Rings nicht ändert:
Aunverpr. = Averpr. (10)
Aunverpr. ist die Querschnittsfläche des unverpressten und Averpr. die des verpressten O-Rings. Während sich Aunverpr. einfach als Kreisfläche berechnen lässt, kann Averpr. in guter Näherung als Kombination aus einer Rechteck- und zwei gleichen Kreissegmentflächen beschrieben werden, vgl. Bild 2. Vorausgesetzt wird hierbei, dass der O-Ring sich seitlich unbehindert ausdehnen kann. Es ist zu beachten, dass die Mittelpunkte der beiden Kreise nicht identisch sind und ebenfalls nicht mit dem Mittelpunkt des Rechtecks übereinstimmen. Die Kreissehne der Kreissegmente entspricht der Höhe t des verpressten O-Rings und kann bei üblichen Dichtungsanwendungen als bekannt vorausgesetzt werden. Hierbei besteht der aus Gl. (2) und Gl. (3) abgeleitete Zusammenhang:
t = d (1 – v) (11)
Alle übrigen Größen, die zur Beschreibung des Kreissegments erforderlich sind, lassen sich in Abhängigkeit vom Radius r formulieren. Somit berechnet sich der Flächeninhalt eines Kreissegments zu:
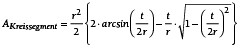 (12)
(12)
Nach Gl. (10) ergibt sich damit:
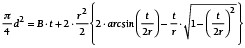 (13)
(13)
Der Radius r des Kreissegments wird auf den Schnurdurchmesser d normiert und im Weiteren als k bezeichnet.
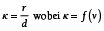 wobei k = f (v) (14)
wobei k = f (v) (14)
Aus den Gleichungen (11), (13) und (14) ergibt sich nach Umformung die auf den Schnurdurchmesser d normierte Berührbreite B des O-Rings zu:
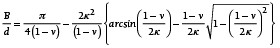 (15)
(15)
Ferner gilt:
s = B + 2a (16)
wobei sich die Höhe a des Kreissegments nach Gl. (17) berechnen lässt.
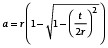 (17)
(17)
Aus Gln. (11), (15), (16) und (17) ergibt sich nach Umformung Gl. (18) zur Ermittlung der Breite des verpressten O-Rings.
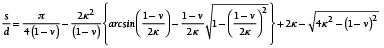 (18)
(18)
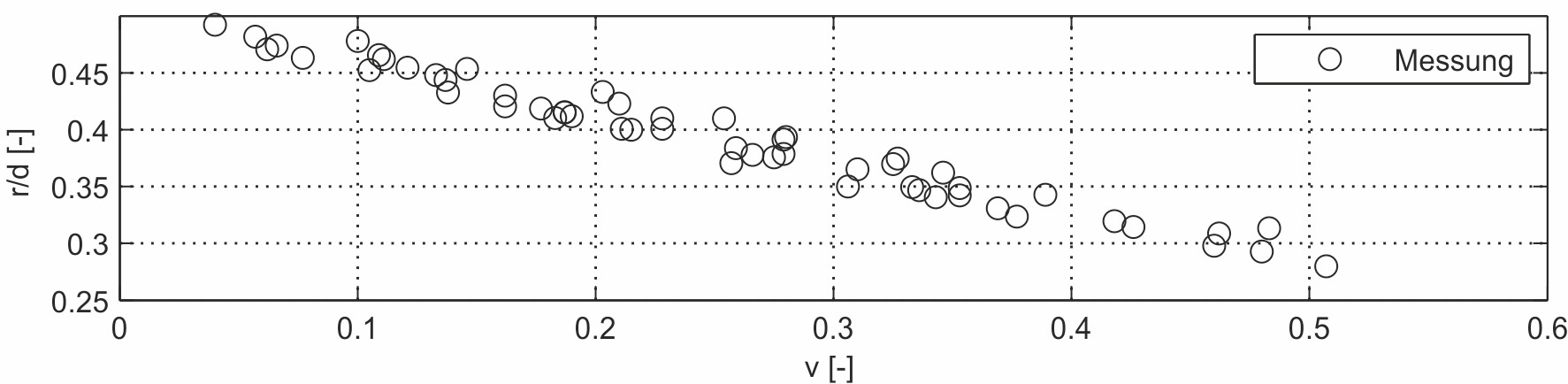
Aus den Gln. (15) und (18) lassen sich die normierte Berühr- bzw. Dichtungsbreite eines O-Rings im verformten Zustand in Abhängigkeit von der Verformung v und des normierten Kreissegmentradius k ermitteln. Die Ergebnisse der Messreihe zeigen, dass sich k als Funktion der Verpressung gut linear approximieren lässt, vgl. Bild 6.
Für den Fall v = 0 gilt r = d/2 und somit k = 1/2. Demnach ergibt sich als Approximationsgleichung:
k(v) = qv + 0,5 (19)
Der Anpassungsparameter q wurde aus den Messdaten ermittelt und beträgt -0,43. Eingesetzt in Gl. (15) bzw. Gl. (18) ergibt sich:
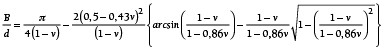 (20)
(20)
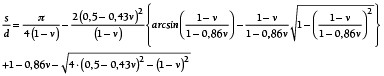 (21)
(21)
Vergleich der unterschied- lichen Methoden mit den Messergebnissen
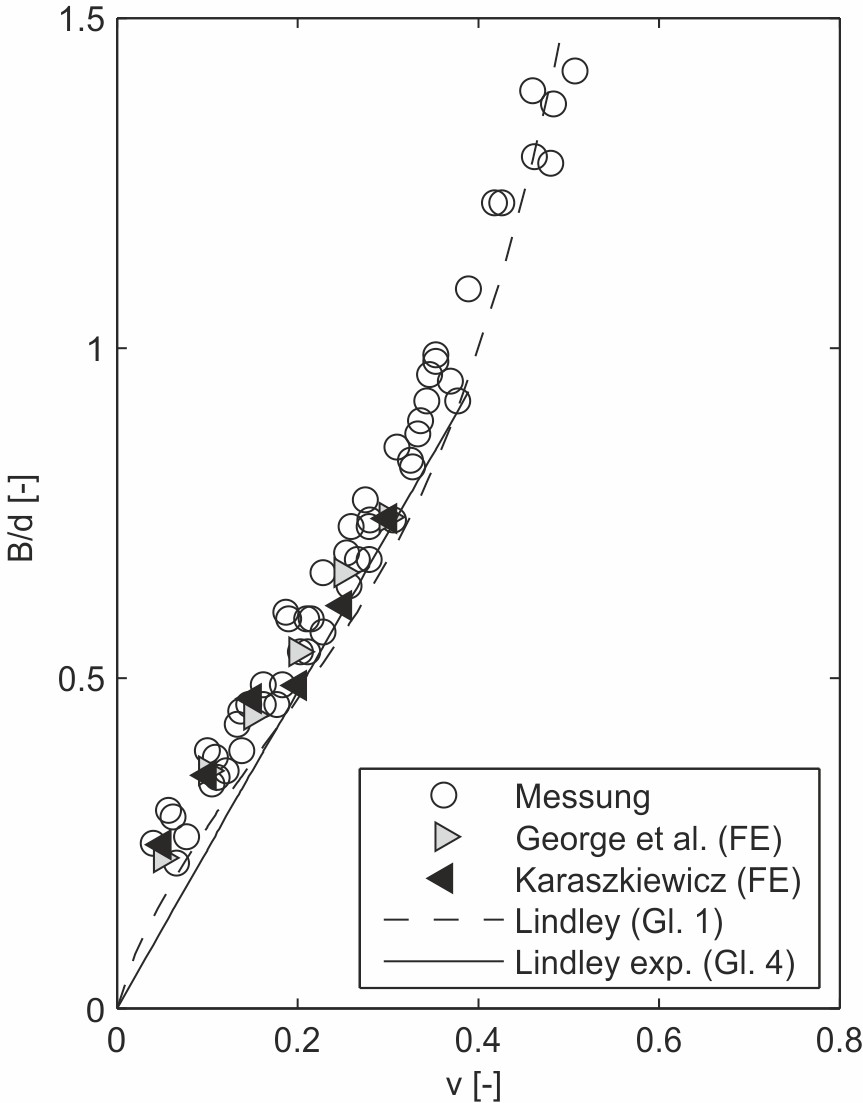
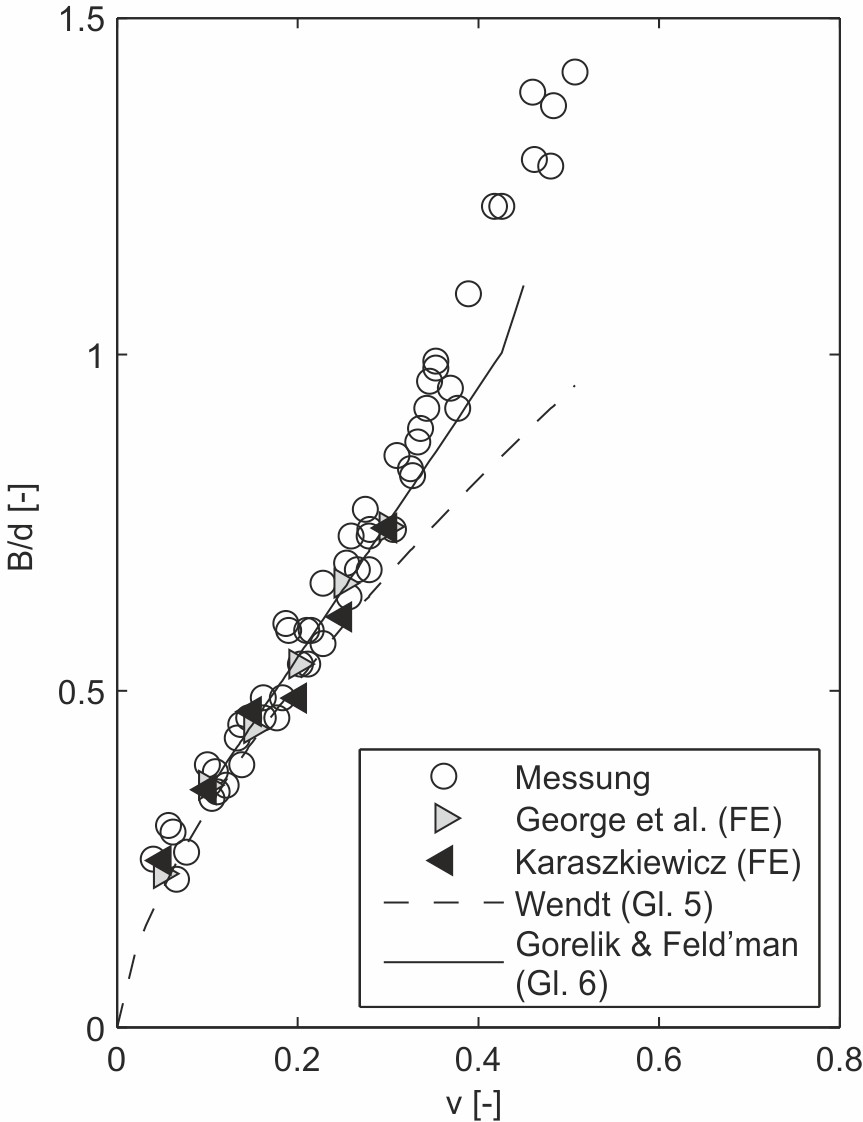
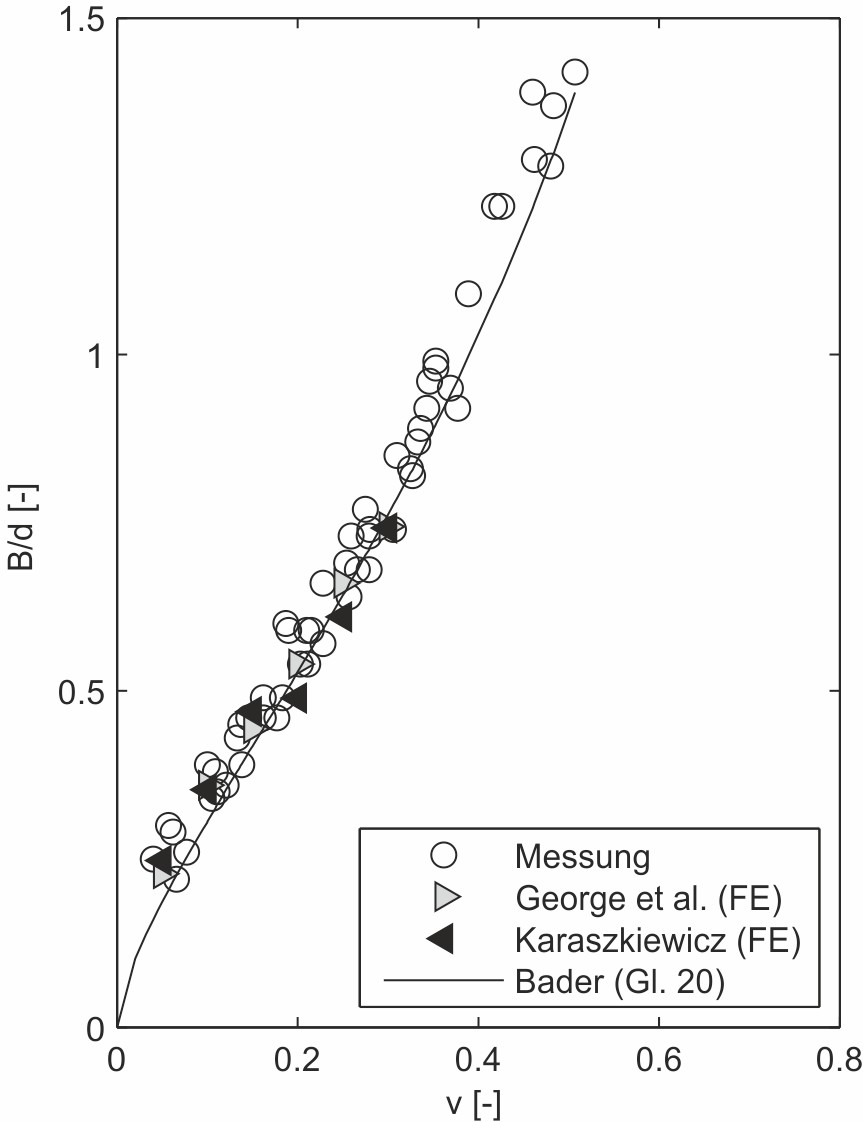
Für einen Vergleich der unterschiedlichen Verfahren zur Bestimmung der O-Ring-Berührbreite werden die experimentell ermittelten Werte sowie die Ergebnisse der Finite Element (FE) Berechnungen von Karaszkiewicz [11] und George et al. [11], [14] als Vergleich herangezogen. In Bild 9 sind die normierten Berührbreiten über der Verpressung aufgetragen. Aus Gründen der Übersichtlichkeit sind die Kurvenverläufe der sechs unterschiedlichen Verfahren in Bild 9a bis d abgebildet.
Bei Verpressungen zwischen 10 % und 30 % weisen die Messdaten einen nahezu linearen Verlauf auf. Die Anwendungsbereiche der linearen Gln. (4), (6) und (7) nach Lindley, Gorelik und Feld’man sowie Karaszkiewicz liegen ungefähr in diesem Bereich. Während Lindleys experimenteller Ansatz insgesamt zu niedrige Berührbreiten liefert, sind die Ergebnisse nach Gorelik und Feld’man mit denen von Karaszkiewicz vergleichbar. Die letztgenannte Methode ist nur für Verpressungen zwischen 7 % und 25 % angegeben, zeigt in diesem Bereich aber eine sehr gute Übereinstimmung mit den Messwerten. Gorelik und Feld’man wählten für ihren Vorschlag einen linearen Zusammenhang bis zu 42,5 % Verpressung. Für größere Verpressungen bis zu 45 % nehmen sie eine quadratische Beziehung an. Allerdings zeigen sich ab 30 % Verpressung deutliche Abweichungen von den Messwerten. Der Ansatz von Wendt gibt die Berührbreite bis zu Verpressungen von ungefähr 25 % gut wieder, weist oberhalb davon aber einen stark unterschiedlichen Verlauf auf. Die von Lindley vorgeschlagene Gl. (1) sowie die hier vorgestellte Methode geben beide den geschwungenen Verlauf der Berührbreite über der Verpressung wieder. Lindleys Formel liefert allerdings bis ca. 45 % Verpressung deutlich zu niedrige Werte. Die nach Gl. (20) ermittelte Kurve zeigt im gesamten Verpressungsbereich die besten Übereinstimmungen mit den experimen- tell ermittelten Berührbreiten sowie den Ergebnissen aus den FE-Berechnungen von George et al. und Karaszkiewicz.
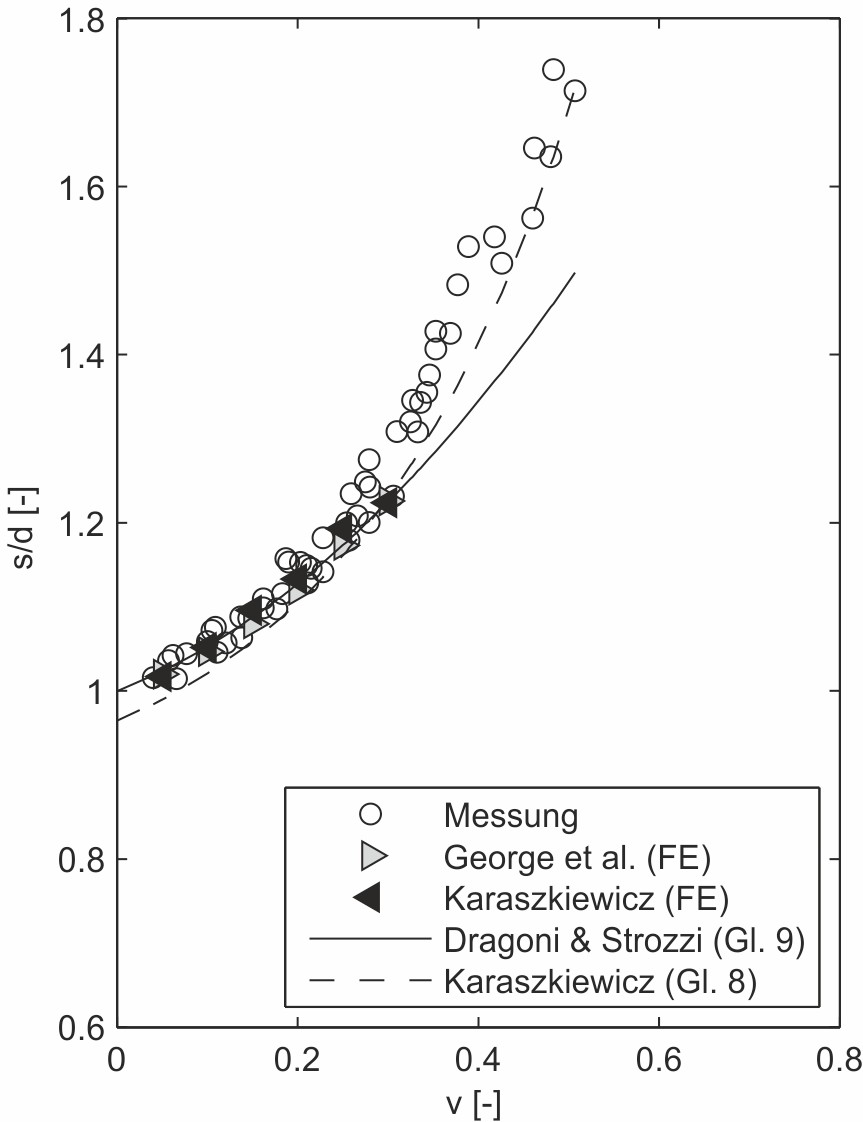
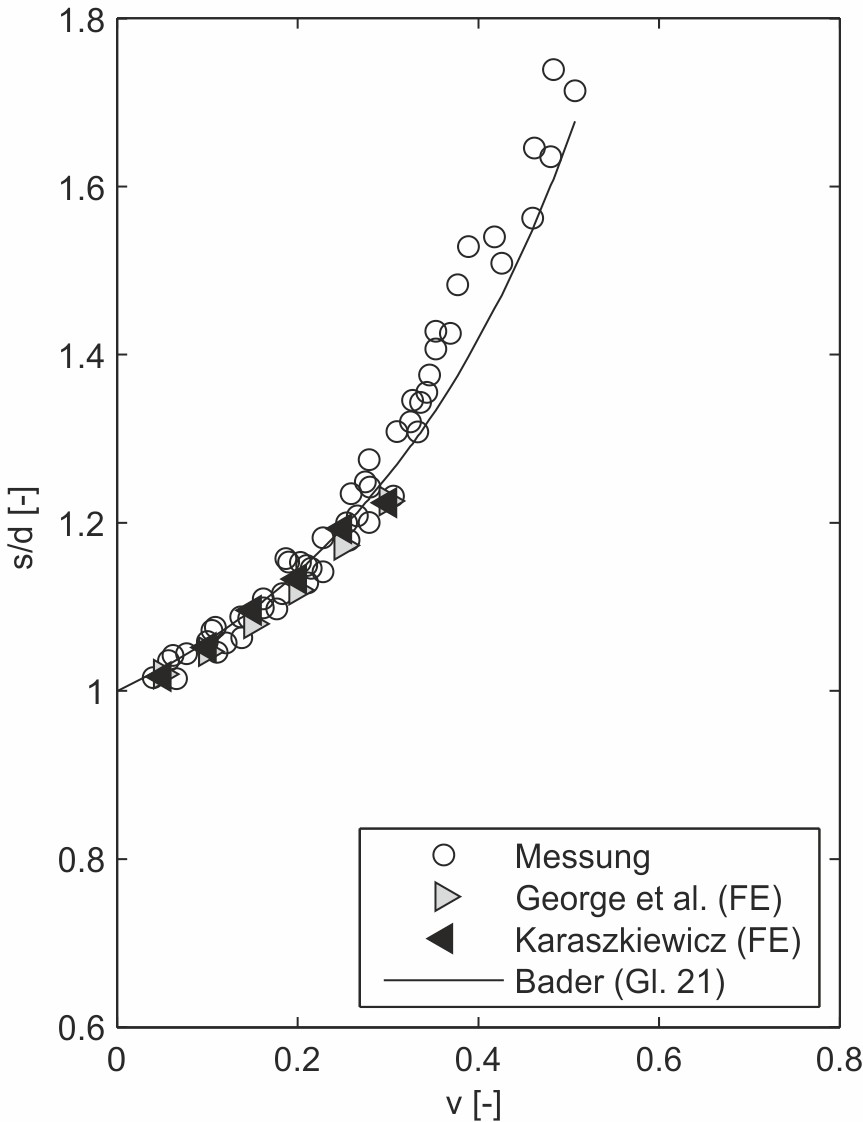
Neben der Berührbreite werden auch die Ansätze zur Ermittlung der verpressten O-Ring-Breite mit den Ergebnissen der Messungen und FE-Berechnungen verglichen. Die Gln. (8) und (9) nach Karaszkiewicz, bzw. Dragoni und Strozzi sind als Kurven in Bild 10a eingetragen.
Für niedrige Verpressungen steht die Methode nach Dragoni und Strozzi in guter Übereinstimmung mit den Messwerten. Oberhalb von ca. 25 % Verpressung jedoch liegen die berechneten Ergebnisse deutlich zu niedrig. Die Kurve nach Karaszkiewicz folgt dem Verlauf der Messwerte im gesamten Verpressungsbereich deutlich besser, liefert aber insgesamt etwas zu niedrige Ergebnisse. Der Vorschlag gemäß Gl. (21) zeigt die beste Übereinstimmung mit den gemessenen Dichtungsbreiten, wobei die Abweichungen bei Verpressungen größer 35 % zunehmen, vgl. Bild 10b. Der Kurvenverlauf ist in diesem Bereich vergleichbar mit der Kurve nach Karaszkiewicz.
Zusammenfassung
Verschiedene in der Literatur beschriebene Verfahren zur Ermittlung der Berühr- sowie der der Dichtungsbreite eines O-Rings bei seitlich unbehinderter Einbausituation wurden zusammengefasst. Weiterhin wurde ein experimenteller Aufbau beschrieben, mit dem die Geometrie von Dichtschnüren bei verschiedenen Verpressungen betrachtet und vermessen werden kann.
Die Ergebnisse dieser bei Raumtemperatur durchgeführten Messungen liegen in sehr guter Übereinstimmung mit den Finite-Element-Rechnungen anderer Untersuchungen. Auswirkungen durch die Elastomerhärte sind hier ebenso wenig auszumachen wie Einflüsse durch die Wahl des Dichtungswerkstoffs.
Ein neuer Ansatz zur Berechnung der Berühr- und Dichtungsbreite, basierend auf der Annahme inkompressibler Dichtungswerkstoffe, wurde vorgeschlagen. Als Eingangsgrößen werden lediglich der Schnurdurchmesser d sowie die Verpressung v des O-Rings benötigt. Beide Größen werden bei der Konstruktion der Dichtstelle festgelegt und können damit direkt in die hergeleiteten Formeln eingesetzt werden.
Die verschiedenen Methoden wurden vergleichend den Messergebnissen gegenüber gestellt, wobei das hier vorgestellte Vorgehen die besten Übereinstimmungen zeigt. Während die anderen Verfahren nur für einen bestimmten Verpressungsbereich gültig sind oder, besonders bei größeren Verpressungen, starke Abweichungen von den gemessenen Werten aufweisen, wird mit diesem Ansatz der Verlauf der Berühr- bzw. Dichtungsbreite im gesamten untersuchten Bereich gut wiedergegeben. Damit bietet sich die Möglichkeit, die O-Ring-Berührbreite für den Fall einer seitlich unbehinderten Ausdehnung bei bekanntem Schnurdurchmesser in Abhängigkeit von der Verpressung mit ausreichender Genauigkeit analytisch zu berechnen.
Literatur
[1] Müller, H. K.; Haas, W.: Dichtungstechnik. Universität Stuttgart, Institut für Maschinenelemente, Vorlesungsmanuskript, 3. Aufl. 2007.
[2] Bader, S.; Haas, W.; Stiegler, B.; Hörl, L.: Statische Dichtungen unter korrosiver Belastung. (Sichere und zuverlässige Dichtverbindungen, XVIII. Dichtungskolloquium, 25./26. September 2013, Rheine). Essen: Vulkan, 2013, S. 162–171.
[3] Bader, S.; Haas, W.; Stiegler, B.: Auslegungskriterien zur Vermeidung korrosiver Durchwanderung statischer Dichtungen. (18th International Sealing Conference, 08./09. Oktober 2014, Stuttgart). Frankfurt a. M.: VDMA Fluidtechnik, 2014, S. 505–519.
[4] Johnson, K. L.: Contact Mechanics. Cambridge : Cambridge University Press, 1985.
[5] Kim, H. ; Park, S. ; Lee, H. ; Kim, D. ; Lee, Y.: Approximation of contact stress for a compressed and laterally one side restrained O-ring. In: Engineering Failure Analysis 14 (2007) Nr. 8, S. 1680–1692.
[6] Lindley, P. B.: Load-compression relationships of rubber units. In: The Journal of Strain Analysis for Engineering Design 1(1966) Nr. 3, S. 190–195.
[7] Lindley, P. B.: Compression characteristics of laterally unrestrained rubber O-ring. In: Journal of International Rubber Institute 1 (1967), S. 202–213.
[8] Green, I.; English, C.: Stresses and deformation of compressed elastomeric O-ring seals. (14th International Conference on Fluid Sealing, Florenz, 1994). London : Mechanical Engineering Publications, 1994, S. 83–95.
[9] Dragoni, E. ; Strozzi, A.: Theoretical analysis of an unpressurized elastomeric O-ring seal inserted into a rectangular groove. In: Wear 130 (1989) Nr. 1, S. 41–51.
[10] Nam, J.; Hawong, J.; Kim, K.; Liu, Y.; Kwon, O.; Park, S.: A study on the development of a loading device using a photoelastic stress freezing method for the analysis of O-ring stress. In: Journal of Mechanical Science and Technology 24 (2010) Nr. 3, S. 693–701.
[11] Karaszkiewicz, A.: Geometry and contact pressure of an O-ring mounted in a seal groove. In: Industrial & Engineering Chemistry Research 29 (1990) Nr. 10, S. 2134–2137.
[12] Dragoni, E.; Strozzi, A.: Analysis of an unpressurized, laterally restrained, elastomeric O-ring seal. In: Transactions of the ASME, Journal of Tribology 110 (1988) Nr. 2, S. 193–200.
[13] Tietze, W.: Handbuch Dichtungspraxis. 3. Aufl., Essen: Vulkan, 2003.
[14] George, A. F.; Strozzi, A.; Rich, J. I.: Stress fields in a compressed unconstrained elastomeric O-ring seal and comparison of computer predictions with experimental results. 11th International Conference on Fluid Sealing; BHRA (British Hydrodynamics Research Association): Crenfield Bedford, England, 1987; paper B1, S. 117–137.
Formelzeichen
AutorenDipl.-Ing. Sascha Bader KonstruktionsingenieurDr.-Ing. Bernd Stiegler Zuverlässigkeitsingenieurbeide: Robert Bosch GmbH Postfach 13 42, 72703 Reutlingen Tel.: 0 71 21/35-3 00 95 E-Mail: sascha.bader@de.bosch.com www.bosch.comProf. Dr.-Ing. habil. Werner Haas Bereichsleiter Dichtungstechnik Dipl.-Ing. Lothar Hörl Technischer Leiterbeide: Universität Stuttgart Institut für Maschinenelemente Pfaffenwaldring 9, 70569 Stuttgart Tel.: 07 11/6 85-6 61 69 E-Mail: werner.haas@ima.uni-stuttgart.de www.ima.uni-stuttgart.de