Methode zur Bestimmung von Hauptkrümmungen in Wälzkontakten
Die Lebensdauer von Maschinenkomponenten mit Wälzkontakten hängt im Wesentlichen von den Belastungen in den Kontaktpunkten ab, welche in den meisten Fällen mit der Hertzschen Theorie berechnet werden. Zur Anwendung der Hertzschen Theorie müssen unter anderem die Hauptkrümmungen im Kontaktpunkt bekannt sein. Für komplexere oder vermessene Komponentengeometrien können diese nicht direkt bestimmt werden, so dass in der Praxis die Hauptkrümmungen ausgehend von der Körpergeometrie angenähert werden. Mit dem vorgestellten Ansatz aus der Differentialgeometrie ist es möglich, für jede Komponentenoberfläche die realen Hauptkrümmungsradien in einem beliebigen Punkt zu bestimmen.
![Bild 1: Zwei allseitig gekrümmte Körper im Kontakt nach [1]. (Bild: WZL RWTH Aachen / Brändlein, Eschmann, Hasbargen, Weigand)](https://www.ingenieur.de/wp-content/uploads/2020/01/KA-557-Brecher-Fey-Hildebrand-Bild1-980x496.jpg)
Bild 1: Zwei allseitig gekrümmte Körper im Kontakt nach [1]. (Bild: WZL RWTH Aachen / Brändlein, Eschmann, Hasbargen, Weigand)
1 Einleitung
Maschinenkomponenten mit Wälzkontakten sind in allen Bereichen der Produktion und des täglichen Bedarfs zu finden. Die Lebensdauer dieser Komponenten ist maßgeblich von den Belastungen in den Wälzkontakten abhängig. In Lagern, Profilschienenführungen, Gewindetrieben oder Zahnradgetrieben wälzen Elemente unterschiedlicher Geometrie aufeinander ab. Infolge der Kontaktkräfte kommt es in den Kontaktbereichen zu Abplattungen und Spannungen, zu deren Berechnung häufig die Theorie nach Hertz angewendet wird. Diese liefert den Wert für die maximale Kontaktnormalspannung, welche zur Beurteilung der Tragfähigkeit sowie der Lebensdauer herangezogen wird, die Annäherung der Körper zueinander, was für die Berechnung der Komponentensteifigkeiten unabdingbar ist, sowie die Größe der Kontaktellipse. Diese ist für die Beurteilung der Kontaktverhältnisse relevant, denn die Kontaktellipsengröße liefert Hinweise auf eine mögliche Einwälzung der Komponentenkanten. Die Anwendung der Hertzschen Theorie erfordert die Kenntnis der Hauptkrümmungen beider Wälzpartner im betrachteten Kontaktpunkt. Während in den einfachen Fällen des Kugel- oder Rollenkontakts mit einer Fläche oder weiterer Kugel/Rolle die Hauptkrümmungen aus der Anschauung heraus einfach zu ermitteln sind, wird dies bei der Betrachtung komplexerer Oberflächen, wie beispielsweise die Flanken einer Gewinderille im Kugel- oder Rollengewindetrieb oder einer Zahnflanke, zu einer nicht trivialen Aufgabe. In diesen Fällen werden die Hauptkrümmungen ausgehend von den geometrischen Abmessungen der Komponenten angenähert, was Abweichungen bei der Berechnung der Pressungen sowie der Halbachsen der elliptischen Kontaktflächen nach sich zieht. Die aus dieser Annäherung resultierenden Berechnungsungenauigkeiten können vermieden werden, indem mit Hilfe eines Ansatzes aus der Differentialgeometrie die tatsächlichen Hauptkrümmungsradien bestimmt werden. Der im Folgenden vorgestellte Ansatz ist auf alle realen Bauteiloberflächen mit bekannter oder vermessener Geometrie anwendbar.
2 Berechnung nach Hertz
Die Hertzsche Theorie geht von zwei beliebig gekrümmten Körpern A und B aus, welche mit einer Kraft F aufeinander gedrückt werden (Bild 1). Infolge der Belastung wird der Werkstoff in der Umgebung des Kontaktpunkts eingedrückt und es entsteht eine Kontaktellipse.
Die maximale Hertzsche Pressung pmax im Kontaktpunkt der dargestellten Körper A und B ergibt sich im Zentrum der Kontaktellipse und kann nach Harris [2] wie folgt berechnet werden:
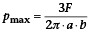
Hierbei sind a und b die Halbachsen der elliptischen Kontaktfläche, welche sich in Abhängigkeit der Poissonzahl v = 0,3, der Summe der Hauptkrümmungen S k sowie der Hertzschen Beiwerte a* und b* ergeben:
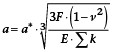
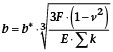
mit:
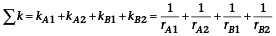
Die Hauptkrümmungen k sind die reziproken Werte der Hauptkrümmungsradien r. Ferner sind diese negativ für konkave Flächen und positiv für konvexe Flächen definiert. Die Beiwerte a* und b* sind abhängig von diesen Hauptkrümmungen und lassen sich entweder mit einer Näherungsfunktion berechnen oder aus Tabellenwerten interpolieren. Die Anwendbarkeit der Hertzschen Theorie setzt voraus, dass die Verbindungslinie der Mittelpunkte der Hauptkrümmungsradien beider Körper senkrecht zur Tangentialebene im Kontaktpunkt steht. Obwohl dieser Zusammenhang bei vielen Kontaktsituationen, wie zum Beispiel in einem Gewinde, nicht zutreffend ist, wird in der Praxis dennoch häufig die Hertzsche Theorie angewendet.
3 Berechnung der Hauptkrümmungen
Wie oben erläutert, ist zur Anwendung der Hertzschen Theorie die Kenntnis der Hauptkrümmungen unabdingbar. Mit den Erkenntnissen aus der Differentialgeometrie ist es möglich, die genauen Hauptkrümmungen in jedem Punkt einer beliebigen Komponentenoberfläche zu bestimmen.
Allgemein gilt, dass für jede reguläre orientierbare Fläche S mit einem Einheitsnormalenfeld n die Eigenwerte der sogenannten Weingartenabbildung W in einem beliebigen Punkt p die Hauptkrümmungen in diesem Punkt der Fläche darstellen [3]. Die Weingartenabbildung ist eine spezielle Funktion der Differenzialgeometrie, welche ausgehend von der Gleichung einer Fläche mit relativ einfachen Rechenoperationen aufgestellt werden kann. Grundsätzlich lässt sich festhalten, dass für jede beliebige reale Komponentenoberfläche eine Weingartenabbildung bestimmt werden kann. Denn alle Komponentenoberflächen sind in der Umgebung eines beliebigen realen Punktes regulär und orientierbar indem sie folgende Voraussetzungen erfüllen:
– bijektiv: jeder Parameterkombination aus der parametrisierten Darstellung der Komponentenoberfläche wird genau ein Punkt auf der Bauteiloberfläche zugeordnet (im Falle von Gewindeflanken darf also maximal eine Windung betrachtet werden).
– stetig differenzierbar (reale Oberflächen beinhalten keine Polstellen).
– für jeden Punkt p ist das Differential der Komponentenoberfläche S injektiv, (an jedem Punkt der Fläche kann eine Tangentialebene angelegt werden).
– auf der ganzen Fläche existiert ein definiertes differenzierbares Einheitsnormalenfeld.
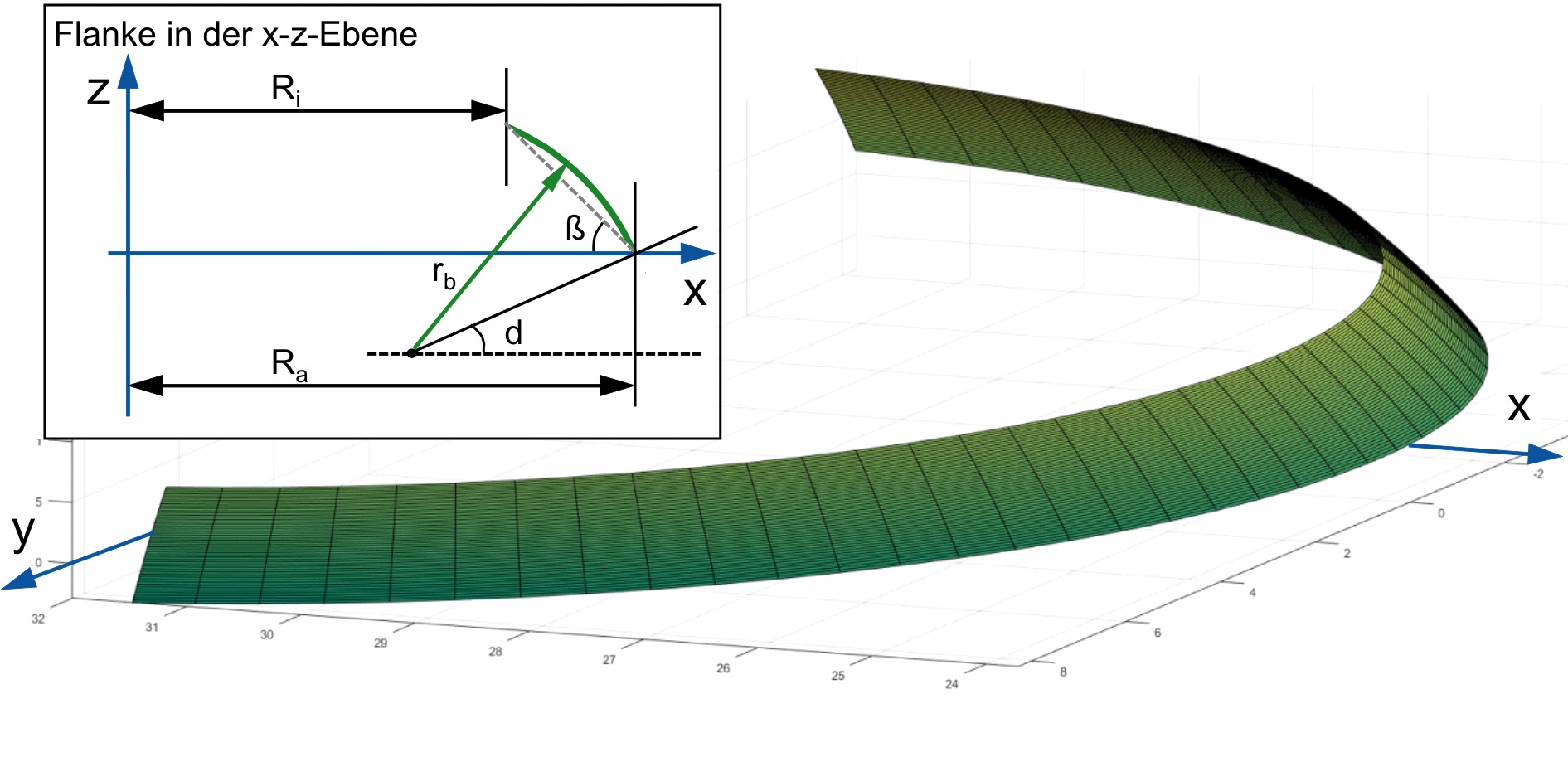
Die Vorgehensweise bei der Berechnung der Hauptkrümmungen soll nun am Beispiel einer balligen Gewindeflanke, wie sie z. B. in Rollengewindetrieben anzutreffen ist, erläutert werden.
Die betrachtete Flanke ist in Bild 2 dargestellt und lässt sich in Anlehnung an [4] durch folgende Funktion beschreiben:
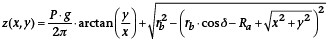
Um das Verfahren anwenden zu können, muss die Funktion der Gewindeflanke in einer Parameterdarstellung der Komponentenoberfläche S vorliegen. Dies ist beispielsweise mit Hilfe der Polarkoordinaten möglich:
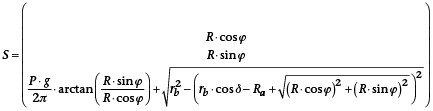
Mit den Parametern R = {m | m ≥ Ri; m ≤ Ra} und j = {a | a ≥ p/2; a ≤ 3p/2}.
Eine weitere Möglichkeit der Parametrisierung ist S = (x, y, z(x,y))T mit den zugehörigen Parametern x und y. Ist die konkrete Funktion der Bauteil- oberfläche unbekannt, so kann diese auch als eine Ausgleichsfläche durch gemessene Oberflächenpunkte dargestellt und anschließend parametrisiert werden.
Die zur Berechnung der Hauptkrümmungen benötigte Weingartenabbildung ist eine 2×2 Matrix, deren Einträge sich aus den Koeffizienten der sogenannten ersten Fundamentalform (E, F, G) sowie der zweiten Fundamentalform (L; M; N) zusammensetzen [3], [5]. Die Fundamentalformen sind ebenfalls Funktionen aus der Differentialgeometrie, mit Hilfe derer Eigenschaften von dreidimensionalen Flächen wie Flächeninhalt eines Flächenstücks oder die Form der Krümmung bestimmt werden können. Die Fundamentalformen haben ebenfalls die Form von 2×2 Matrizen, deren Koeffizienten anhand von partiellen Ableitungen der Parameterdarstellung berechnet werden.
Die Koeffizienten der ersten Fundamentalform ergeben sich aus den Skalarprodukten der partiellen Ableitungen zu:
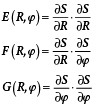
Die Koeffizienten der zweiten Fundamentalform werden aus dem Einheitsnormalenfeld n und den Ableitungen zweiter Ordnung von S gebildet. Das Einheitsnormalenfeld ist das normierte Kreuzprodukt der partiellen Ableitungen von S nach den beiden Parametern, im vorliegenden Beispiel R und j:
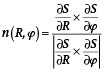
Für die Koeffizienten der zweiten Fundamentalform gilt:
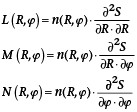
Die Weingartenabbildung W ist definiert als:
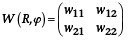
mit:
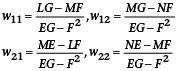
Um die Hauptkrümmung im Punkt p zu berechnen, müssen die Parameter des Punkts p (Rp und jp) in die Weingartenabbildung eingesetzt werden.
Im folgenden soll exemplarisch ein (idealer) Kontaktpunkt zwischen zwei balligen Gewindeflanken A und B, wie sie in einem Rollengewindetrieb vorkommen, betrachtet werden. Die Gewindeparameter der beiden Flanken sind in der Tabelle 1 zusammengefasst.
| Gewindeflanke A | Gewindeflanke B | |
| Gewindeteilung P | 3 | 3 |
| Anzahl der Gewindegänge g | 1 | 5 |
| Äußerer Gewinderadius Ra | 7,25 | 20,25 |
| Innerer Gewinderadius Ri | 5,75 | 17,25 |
| Balligkeitsradius rb | 2,025 | 5 |
| Flankenwinkel b | 45° | 45° |
| Lagewinkel d des äußeren Gewindepunkts | 29,2° | 36,46° |
| Parameter Rp des Kontaktpunkts p | 6,5 | 19,5 |
| Parameter jp des Kontaktpunkts p | p | p |
Tabelle 1: Im Berechnungsbeispiel verwendete Gewindeparameter
Für die Gewindeflanke A ergibt sich die Weingartenabbildung im Punkt p (6,5; p) zu:
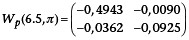
Die Hauptkrümmungen k1 und k2 der Gewindeflanke A im Punkt p sind die Eigenwerte l1 und l2 der Weingartenabbildung im Punkt p:
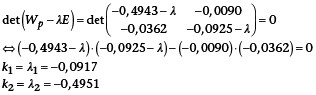
Die Vorzeichen der Eigenwerte hängen von der Orientierung der Komponentenoberfläche im Raum bezüglich der Koordinatenachsen ab. So ergeben sich bei der Richtungsumkehr der z-Achse positive, betragsmäßig gleiche, Hauptkrümmungen. Für die Anwendung in der Berechnung nach Hertz sind daher nur die Beträge der Hauptkrümmungen verwertbar. Die Zuordnung der Vorzeichen entsprechend konvexen und konkaven Flächen muss separat durchgeführt werden.
Die Hauptkrümmungsradien ergeben sich aus dem Kehrwert der Beträge der Eigenwerte, im vorliegenden Beispiel zu:
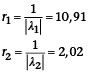
| Realer Wert
in mm |
Näherung
in mm |
Abweichung
in % |
|
| Hauptkrümmungsradius rA1 (entspricht Rp / cos45°) | 10,91 | 9,19 | 15,77 |
| Hauptkrümmungsradius rA2 (entspricht Balligkeitsradius) | 2,02 | 2,03 | 0,50 |
| Hauptkrümmungsradius rB1 (entspricht Rp / cos45°) | 28,24 | 27,58 | 2,34 |
| Hauptkrümmungsradius rB2 (entspricht Balligkeitsradius) | 5,00 | 5,00 | 0,0 |
| Maximale Pressung pmax
(in N/mm2) |
1417,4 | 1464,5 | 3,32 |
| Große Halbachse der Kontaktellipse a | 0,1016 | 0,0957 | 5,81 |
| Kleine Halbachse der Kontaktellipse b | 0,0332 | 0,0341 | 2,71 |
Tabelle 2: Vergleich der Hertzschen Parameter bei der Berechnung mit realen und angenäherten Hauptkrümmungsradien
Es wird deutlich, dass der zweite Krümmungsradius mit r2 = 2,02 den Balligkeitsradius der Gewindeflanke mit rb = 2,025 widerspiegelt, wobei die minimale Abweichung sich aufgrund des Gewindesteigungswinkels ergibt. Der erste Hauptkrümmungsradius r1 wurde bei der bisher üblichen Vorgehensweise mit Hilfe von Rp sowie dem Flankenwinkel b = 45° wie folgt angenähert: r1 = Rp / cos 45° = 9,19 [6]. Beim ersten Hauptkrümmungsradius ergibt sich damit bereits eine Abweichung von 15,77 % zum realen Wert von r1 = 10,91. Die Abweichung nimmt mit steigendem Balligkeitsradius der Gewindeflanke zu. Die Differenzen der Werte, welche infolge der Abschätzung der Krümmungsradien entstehen, können der Tabelle 2 entnommen werden.
Verwendete Formelzeichen:
| a: | Große Halbachse der Kontaktellipse |
| a*: | Hertzscher Beiwert |
| b: | Kleine Halbachse der Kontaktellipse |
| b*: | Hertzscher Beiwert |
| E, F, G: | Koeffizienten der ersten Fundamentalform |
| g: | Anzahl der Gewindegänge |
| k1, k2: | Hauptkrümmungen |
| L, M, N: | Koeffizienten der zweiten Fundamentalform |
| n: | Einheitsnormalenfeld |
| P: | Gewindeteilung |
| p: | ein beliebiger Punkt auf der Komponentenoberfläche |
| pmax: | Maximale Hertzsche Pressung im Kontakt |
| R: | Radius |
| r1, r2: | Hauptkrümmungsradien |
| Ra: | Äußerer Gewinderadius |
| rb: | Balligkeitsradius |
| Ri: | Innerer Gewinderadius |
| S: | Parameterdarstellung einer Fläche |
| W: | Weingartenabbildung |
| w11, w12, w21, w22: | Koeffizienten der Weingartenabbildung |
| b: | Flankenwinkel |
| d: | Lagewinkel des äußeren Gewindepunkts |
| l1, l2: | Eigenwerte der Weingartenabbildung |
| j: | Winkel |
Die deutlichste Abweichung unter den Ergebnissen ergibt sich im vorliegenden Beispiel für die Abmessung der großen Halbachse der Kontaktfläche mit fast 6 %.
Fazit
Die vorgestellte Berechnungsgrundlage ist universell auf jede Komponentenoberfläche anwendbar und liefert genaue Werte der Hauptkrümmungen in jedem beliebigen Punkt der Ober-fläche. Dadurch können Ungenauigkeiten, welche bei der Berechnung von Kontaktpunktverhältnissen durch eine Abschätzung der Hauptkrümmungen entstehen, vermieden werden. Aufgrund des Berechnungsaufwands ist die vorgestellte Methode besonders für komplexe Geometrien, welche eine verlässliche Abschätzung der Krümmungen nicht erlauben, geeignet. Ferner können mit diesem Ansatz auch Hauptkrümmungen von zuvor vermessenen realen Oberflächen, beispielsweise von Komponentenlaufbahnen, die durch Verschleiß verändert wurden, bestimmt werden. Hier-zu werden die Oberflächen messtechnisch abgetastet und die Messpunkte durch eine (gekrümmte) dreidimensionale Fläche angenähert. Die Hauptkrümmungen der nun mathematisch bekannten Näherungsfläche können mit Hilfe des vorgestellten Verfahrens berechnet werden, so dass verschleißbedingte Veränderungen der Hertzschen Pressung oder der Größe der Kontaktellipse beurteilt werden können.
Danksagung: Die Autoren danken der Deutschen Forschungsgemeinschaft (DFG) für die finanzielle Unterstützung des Forschungsvorhabens „Untersuchung des Betriebsverhaltens von Planetenrollengewindetrieben mit unterschiedlicher Gewindegangzahl der Spindel und der Mutter“ (Kennzeichen BR 2905/54-1). Die hier präsentierten Forschungsergebnisse wurden in diesem Projekt erarbeitet.
Autoren Prof. Christian Brecher Leiter des Lehrstuhls für Werkzeugmaschinen Dr.-Ing. Marcel Fey Oberingenieur Dipl.-Ing. Maria Hildebrand Wissenschaftliche Mitarbeiterinalle: Werkzeugmaschinenlabor RWTH-Aachen WZL Steinbachstraße 19 52074 Aachen Tel.: 02 41/80-2 62 86 E-Mail: m.hildebrand@wzl.rwth-aachen.de www.wzl.rwth-aachen.deLiteratur