Abschätzung der Staubungsneigung von trockenen Schüttgütern
Die zumeist unerwünschte Freisetzung von Partikeln aus Schüttgütern kann bei den unterschiedlichsten Handhabungen der Materialien erfolgen und eine Gefährdung für Mensch und Umwelt sein. Die Staubungsneigung ist somit eine wichtige Eigenschaft eines Materials und dabei abhängig von der jeweiligen Art der Beanspruchung. Eine Prognose über die Staubungsneigung könnte die Abschätzung eines möglichen Gefährdungspotenzials vereinfachen und beschleunigen, da auf umfangreiche Versuche verzichtet werden kann. In der hier vorliegenden Arbeit wurde die Staubungsneigung von neun unterschiedlichen Materialien mit einer Rotationsapparatur untersucht. Anhand der ermittelten Ergebnisse und unter Berücksichtigung der Messmethodik und der apparativen Geometrie konnte ein apparaturspezifischer Kennwert entwickelt werden. Mithilfe dieses Kennwertes gelang es, empirische Prognosefunktionen für eine Rotationsapparatur abzuleiten.

Bild 2. Rotationsapparatur Dustmeter der Fa. Heubach; (a) Steuereinheit und Antriebsmotor, (b) Staubentwicklungsgefäß (Rotationstrommel), (c) Grobabscheider, (d) Filtergehäuse mit Filter.
Foto: Bergische Universität Wuppertal
Foto: Bergische Universität Wuppertal
1 Einführung
Die Tendenz eines trockenen Materials, bei einer bestimmten Handhabung Partikel freizusetzen, wird nach [1] als Staubungsneigung eines dispersen Feststoffsystems verstanden. Die unkontrollierte und unerwünschte Freisetzung von Partikeln kann zu einer Belastung und/oder Gefährdung von Personen, zur Verschmutzung der Umwelt oder zum Verlust einer wichtigen Materialressource führen. Daher ist es hilfreich, eine mögliche Exposition bereits vor der Handhabung des Materials anhand von Informationen zur Staubungsneigung, die auf material-, verteilungs- und/oder prozessspezifischen Parametern beruhen, abschätzen zu können.
Der Energieeintrag in Pulver, der maßgeblich für die Freisetzung von Partikeln verantwortlich ist, wird insbesondere über das Verhältnis der einwirkenden Haft- und Trennkräfte bestimmt. Daher bewirken unterschiedliche Handhabungen von Pulvern (z. B. Umfüll- oder Mischvorgänge) unterschiedliche Staubfreisetzungen. Die Staubungsneigung ist somit sowohl vom Material (interpartikuläre Haftkräfte), als auch vom Prozess (Trennkräfte) abhängig [2 bis 4]. Zur Simulierung der unterschiedlichen Handhabungen und zur reproduzierbaren Charakterisierung der Staubungsneigung eines Materials werden deshalb auch unterschiedliche Laborapparaturen eingesetzt.
2 Experimentelles Vorgehen und Versuchsaufbau
2.1 Testmaterialien
Zur Untersuchung der Staubungsneigung von Pulvern wurden neun verschiedene Testmaterialien verwendet. Um allgemeingültige Aussagen bzw. Vorhersagen zur Staubfreisetzung bei unterschiedlichen Handhabungen treffen zu können, wurde bei der Auswahl der Testmaterialien darauf geachtet, dass diese ein möglichst breites Spektrum an material- und verteilungsspezifischen Eigenschaften abdecken. Folgend sind die verwendeten Testmaterialien sowie deren Abkürzungen aufgelistet:
- Arizona A1 bis A4 (A1 bis A4)
- Baustellenschmutz (Bau)
- ECE R-45 (ECE)
- KSL 11047 (KSL)
- Pural NF (Pural)
- Ulmer Weiss XMF (UW)
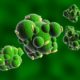
Bild 1 zeigt mit einem Environmental Scanning Electron Microscope (ESEM) aufgenommene Bilder der Testmaterialien.

Bild 1. Aufnahmen mit einem Rasterelektronenmikroskop der verwendeten Versuchsmaterialien.
Foto: Bergische Universität Wuppertal
Die Testmaterialien Arizona A1 (ultrafein), A2 (fein), A3 (mittel) und A4 (grob) bestehen zu mindestens 98 % aus Siliciumdioxid (SiO2) [5]. Der Prüfstaub Baustellenschmutz ist eine Mischung aus den vier Komponenten Sand, Gips, Ziegelstaub und Zement (jeweils 25 %) [6]. Das Testmaterial ECE R-45 besteht ebenfalls aus verschiedenen Komponenten, wobei die Hauptkomponenten Siliciumdioxid (88 %) und pflanzlicher Kohlenstaub (10 %) sind [7]. Die Testpulvermischung KSL 11047 dient zur Simulation von Hausstaub und enthält deshalb neben der Hauptkomponente Siliciumdioxid (37 bis 72 %) auch Anteile von Viskosefasern (2,5 bis 40 %) und Baumwollfasern (1,35 bis 10 %) sowie einen geringen Anteil weiterer Komponenten [8]. Der Teststaub Pural NF besteht aus Aluminiumoxid (77 %), Natriumoxid (Na2O; 0,002 %) und Wasser (H2O; 22,998 %), das im kristallinen Festkörper gebunden ist [9]. Das Testmaterial Ulmer Weiss XMF (UW) besteht zu über 99 % aus Calciumcarbonat (CaCO3) [10].
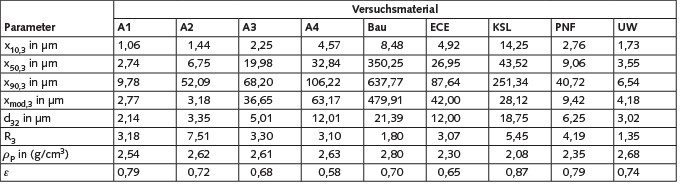
In Tabelle 1 sind relevante Parameter der verwendeten Versuchsmaterialien aufgeführt.
Dabei handelt es sich um den massebezogenen Medianwert (x50,3) und Modalwert (xmod,3) sowie das 10-%-Perzentil (x10,3) und 90-%-Perzentil (x90,3) der untersuchten Verteilungen. Des Weiteren den Sauterdurchmesser d32, der den Durchmesser von Partikeln eines monodispersen Stoffsystems angibt, dessen Gesamtvolumen und Oberfläche genauso groß ist wie in einem polydispersen Stoffsystem (vgl. Gl. 1) [11; 12]. In diesem Zusammenhang wurde ein für eine Verteilung spezifischer Kennwert, das Moment M-1,3, verwendet. Das Moment ist eine mathematische Unterstützung zur Umrechnung der Mengenarten von Verteilungsfunktionen und ihrer spezifischer Kennwerte.
Die Spanne R3 einer Verteilung wird üblicherweise aus der Differenz zwischen dem x90,3– und x10,3-Wert gebildet [13]. Bei der hier durchgeführten Arbeit wurde diese Differenz auf den Medianwert der Verteilung bezogen (vgl. Gl. 2).
Die Porosität e beschreibt das Verhältnis des Hohlraumvolumens zwischen den Partikeln bezogen auf das Gesamtvolumen. Berechnet wurde die Porosität nach Gl. 3 mit der Schüttdichte rS und der Partikeldichte rP [12; 14].
Die Testmaterialien wurden 24 h bei 105 °C in einem Trockenofen getrocknet.
2.2 Rotationsapparatur
Die Staubfreisetzung der Testmaterialien wurde mit der in Bild 2 dargestellten Rotationsapparatur ermittelt [15].

Bild 2. Rotationsapparatur Dustmeter der Fa. Heubach; (a) Steuereinheit und Antriebsmotor, (b) Staubentwicklungsgefäß (Rotationstrommel), (c) Grobabscheider, (d) Filtergehäuse mit Filter. Quelle : Bergische Universität Wuppertal Quelle : Bergische Universität Wuppertal
Die Probenaufgabe erfolgt diskontinuierlich, bei anschließender periodischer Probenbeanspruchung mit kontinuierlicher Probenahme und gravimetrisch fraktionierter Auswertung.
Das Staubentwicklungsgefäß (vgl. Bild 2 (b)) mit einem Durchmesser von 140 mm wird mit der zu untersuchenden Probe befüllt. Bei den hier durchgeführten Untersuchungen betrug die Masse der untersuchten Probe 50 g. In der Rotationstrommel befinden sich drei Umlenkbleche. Die Rotation der Trommel übt eine mechanische Beanspruchung auf das Versuchsmaterial aus. Eine Anhaftung von Material an den Innenwänden der Rotationstrommel wird durch Klopfer, die an der Außenseite der Trommel befestigt sind, verhindert. Das Staubentwicklungsgefäß wird mit der Befestigungswelle an die Steuereinheit (vgl. Bild 2 (a)) angeschlossen.
An der Befestigungswelle selbst befinden sich drei Lufteinlassöffnungen, sodass unter Verwendung einer im System integrierten Vakuumpumpe ein Luftstrom erzeugt werden kann, der den durch die Rotation der Trommel generierten Staub aus dem Staubentwicklungsgefäß austrägt. Der mit Partikeln beladene Volumenstrom passiert zunächst einen Grobabscheider (vgl. Bild 2 (c); Sedimentationsflasche) und erreicht anschließend den Filter (vgl. Bild 2 (d)). Als Filter wurden Glasfaserfilter der Fa. Whatman verwendet (Grad GF 92).
Über das Massenverhältnis des ausgetragenen Staubes (Differenz des Filters vor (m1) und nach der Messung (m2)) zur aufgebrachten Probenmenge m0 wird die Staubungsneigung berechnet (vgl. Gl. 4).
Für die Untersuchungen wurde das Dustmeter der Fa. Heubach verwendet.
Die Testmaterialien wurden im getrockneten Zustand in die Rotationsapparatur eingebracht.
3 Ergebnisse
3.1 Staubungsneigung
Die mit Gl. 4 berechneten Staubmaßzahlen (Staubungsneigung) für die Testmaterialien sind zusammen mit ihren Standardabweichungen in Bild 3 dargestellt.
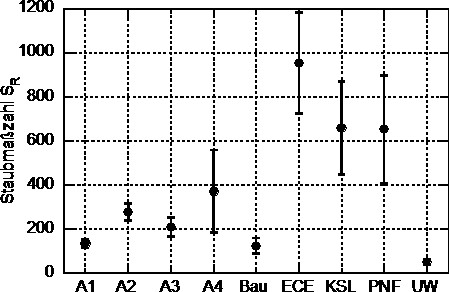
Bild 3. Darstellung der Staubmaßzahl (trocken) der Untersuchungen mit der Rotationsapparatur für die verwendeten Versuchsmaterialien. Quelle : Bergische Universität Wuppertal
Es ist zu erkennen, dass die verwendeten Testmaterialien bei der Beanspruchung in der Rotationsapparatur eine breite Spanne in Bezug auf die Staubungsneigung aufwiesen (SR von ca. 51 (UW) bis ca. 954 (ECE)). Die Stoffe A1, A2, A3, Bau und UW hatten eine geringere Staubungsneigung als die Stoffe A4, ECE, KSL und PNF, wobei die zweite Gruppe auch höhere Standardabweichungen aufwies. Da die Testmaterialien eine breite Spanne von material- bzw. verteilungsspezifischen Parametern abdeckten, war der direkte Vergleich bezüglich eines einzigen Parameters (wie z. B. des Modalwertes, des Medianwertes oder der Porosität) nicht aussagekräftig. Eine Ausnahme bildeten die Arizona-Stäube, die die gleichen materialspezifischen Eigenschaften haben und sich nur in der Partikelgrößenverteilung unterscheiden. Somit könnten hier Rückschlüsse auf den Einfluss der Partikelgrößenverteilung hinsichtlich der Staubungsneigung geschlossen werden. Zu beobachten war ein Trend zu steigender Staubungsneigung mit Verschiebung der Partikelgrößenverteilung zu größeren Partikeln, die in ähnlichem Kontext auch für quarzhaltige Mineralien bis zu 25 µm gefunden wurde [16].
3.2 Prognosekennwert
Um für derart unterschiedliche Schüttgüter die Staubungsneigung bei der Beanspruchung durch die Rotationsapparatur prognostizierbar zu machen, wurde anhand von material- und verteilungsspezifischen Parametern aus den Versuchen ein semiempirischer Kennwert KRA entwickelt (vgl. Gl. 5).
Dieser Kennwert KRA wird aus der Porosität e der Schüttung, der Spanne R3, dem Sauterdurchmesser d32 aller Partikeln und dem Sauterdurchmesser aller Partikel, die größer als die Grenzpartikelgröße d32,Gp sind, gebildet.
Der Entwicklung des Kennwertes KRA liegen folgende Überlegungen zugrunde:
Mithilfe der modellhaften Ermittlung von Geschwindigkeiten, die die Wirbelgeschwindigkeiten in der Rotationsapparatur reflektieren, werden für die Staubungsneigung relevante Grenzpartikelgrößen Gp berechnet. Um Anhaltspunkte für die Grenzpartikelgröße zu erhalten, wurde davon ausgegangen, dass durch die Vorgänge in der Rotationstrommel eine turbulente Strömung erzeugt wird. Eine turbulente Strömung beschreibt eine Strömungsform, die nicht in geordneten Fluidbahnen verläuft, sondern durch entstehende Wirbel ein instationäres System bildet [17]. Die Wirbel bewegen sich mit einer entsprechenden Umlaufgeschwindigkeit uW. Diese Umlaufgeschwindigkeit ist abhängig von der Strömungsgeschwindigkeit des Fluides uS, der Größe des Wirbels lW und der kinematischen Viskosität des Fluides v und kann mit Gl. 6 abgeschätzt werden [19].
Die Größe des kleinsten Wirbels k wiederum ist im Bereich der Mikroskala abhängig von der Strömungsgeschwindigkeit im System uS, der kinematischen Viskosität v und der Größe des größtmöglichen Wirbels lW (vgl. Gl. 7) [18].
Die Größe des größten Wirbels ist durch die Abmessung der Rotationstrommel (Durchmesser: 0,14 m) gegeben. Über den verwendeten Volumenstrom von 20 l/min und die Berechnung der kreisrunden Anströmfläche der Rotationstrommel kann die Strömungsgeschwindigkeit in der Rotationstrommel berechnet werden (uS = 21,65 · 10–3 m/s). Mit einer kinematischen Viskosität von 15,3 · 10–6 m2/s ergibt sich für den größten Wirbel die Umlaufgeschwindigkeit 5,77 · 10–3 m/s, für den kleinsten Wirbel 15,56 · 10–3 m/s.
Zur Bildung eines Verhältnisses zwischen der Wirbelgeschwindigkeit und der Sinkgeschwindigkeit nach Stokes ws,St wurde die Annahme getroffen, dass die Wirbelgeschwindigkeit der Sinkgeschwindigkeit nach Stokes entspricht und gemäß Gl. 8 die äquivalente Partikelgröße berechnet werden kann. Der Stokesdurchmesser xSt wird unter Berücksichtigung der dynamischen Viskosität n, der Partikeldichte, der Dichte des umgebenden Fluides rF, der Erdbeschleunigung g und der Sinkgeschwindigkeit nach Stokes berechnet. Der Stokes-Bereich ist gegeben, wenn die Reynoldszahl Re < 0,25 ist [11; 12].
Es wurde nun die Annahme getroffen, dass ein Partikel, dessen Größe der der äquivalenten Sinkgeschwindigkeit nach Stokes (vgl. Gl. 8) entspricht, als Grenzpartikelgröße geeignet ist. Partikeln mit einer höheren Sinkgeschwindigkeit bringen einen genügend hohen Impuls auf, um den Wirbel zu verlassen. Unter Anwendung der materialspezifischen Parameter aller Versuchsmaterialien wurde für den größten Wirbel aus dessen äquivalenter Sinkgeschwindigkeit ein Partikelgrößenbereich von 8,3 bis 9,6 µm und für den kleinsten Wirbel ein Partikelgrößenbereich von 13,6 bis 15,8 µm ermittelt. Als Grenzpartikelgrößen ergaben sich daraus 8,8 µm für den größten und 13,2 µm für den kleinsten Wirbel, da diese die nächsten Intervallgrenzen der ermittelten Partikelgrößenverteilungen waren.
Anhand der ermittelten Grenzpartikelgröße wird die Partikelgrößenverteilung des Materials geteilt. Zur Berechnung des entsprechenden Sauterdurchmessers d32,Gp werden nur die Partikel berücksichtigt, die oberhalb der Grenzpartikelgröße liegen.
3.3 Prognosefunktionen
In Tabelle 2 sind die aus den Versuchen abgeleiteten Regressionsfunktionen dargestellt, mit deren Hilfe unter Nutzung des Kennwertes KRA die Staubmaßzahl SR bei Beanspruchung in der Rotationsapparatur prognostiziert werden kann.
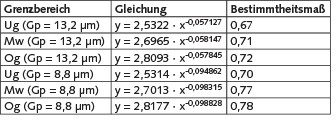
Tabelle 2. Darstellung der Regressionsfunktion mit dem dazugehörendem Bestimmtheitsmaß für unterschiedliche Grenzen mit den Grenzpartikelgrößen 13,2 µm und 8,8 µm.
Die unterschiedlichen Grenzen, abgeleitet aus den ermittelten Standardabweichungen stellen die Untergrenze (Ug), den Mittelwert (Mw) und die Obergrenze (Og) dar. Zur Ermittlung dieser Daten wurde die logarithmierte Staubmaßzahl SR bezogen auf den Kennwert KRA aufgetragen. Der von der Grenzpartikelgröße abhängige Sauterdurchmesser d32,Gp wurde zum einen mit einer Grenzpartikelgröße von 13,2 µm und zum anderen mit einer Grenzpartikelgröße von 8,8 µm berechnet.
Es ist zu erkennen, dass mit Abnahme der Grenzpartikelgröße das Bestimmtheitsmaß für die Regressionsfunktionen zunimmt. Aus diesem Grund wurden die Berechnungen für weitere Grenzpartikelgrößen durchgeführt. Das höchste Bestimmtheitsmaß lieferte hier eine Grenzpartikelgröße von 2,9 µm (vgl. Bild 4).
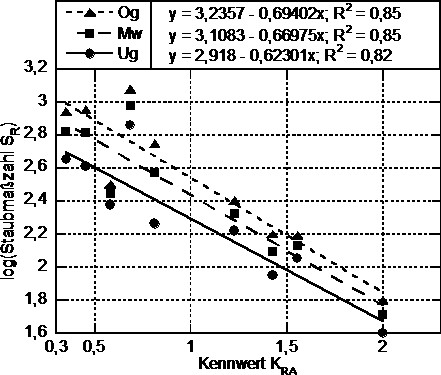
Bild 4. Darstellung der logarithmierten Staubmaßzahl für die Untergrenze (Ug), den Mittelwert (Mw) und die Obergrenze (Og) bezogen auf den Kennwert KRA für die Rotationsapparatur mit der Grenzpartikelgröße von 2,9 µm; mit Angabe der entsprechenden Regressionsfunktion mit Bestimmtheitsmaß. Quelle : Bergische Universität Wuppertal
Im Folgenden sind die wichtigsten Grenzbedingungen aufgeführt, für die Gl. 5 keine Gültigkeit besitzt:
Die Partikelgrößenverteilung weist keine Partikel größer als der Grenzpartikeldurchmesser von 2,9 µm auf, denn dadurch wären d32,Gp und d32 gleich groß.
Die Porosität darf weder 1 noch 0 betragen.
In Bild 4 ist die logarithmierte Staubmaßzahl SR bezogen auf den Kennwert KRA aufgetragen. Für die verschiedenen Grenzbereiche sind jeweils die entsprechenden Regressionsfunktionen und das Bestimmtheitsmaß dargestellt.
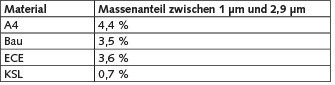
Durch die Veränderung der Grenzpartikelgröße auf 2,9 µm weisen alle Grenzbereiche nun eine höhere Übereinstimmung mit den Regressionsfunktionen auf. Dies könnte am Trägheitseffekt bei kleineren Grenzpartikeln liegen. Der Trägheitseffekt besagt, dass Partikel aufgrund ihrer Masse nicht der Fluidbahn folgen und somit auch nicht der Strömung. Der Trägheitseffekt tritt ab Partikelgrößen von etwa 1 µm auf [19]. Es wurde weiterhin festgestellt, dass durch eine weitere Verkleinerung der Grenzpartikelgröße das Bestimmtheitsmaß wieder abnimmt. Dies ist plausibel, da vier der neun verwendeten Materialien in dem Intervall zwischen 1 und 2,9 µm einen geringen Prozentsatz an der gesamten Materialmasse aufweisen. In Tabelle 3 sind die entsprechenden Massenanteile dargestellt.
Das bedeutet dann auch, dass bei einer Gesamtbetrachtung aller Materialien die Massenanteile, die ≤ 2,9 µm entsprechen, unterrepräsentiert sind und daher das Bestimmtheitsmaß ab dieser Grenzpartikelgröße ein Optimum aufweist. In diesem Zusammenhang konnte bei Untersuchungen zur Staubungsneigung von Pulvern, deren mittlere Partikelgröße anstieg, gezeigt werden, dass für den Bereich zwischen 3 und 10 µm die Staubung mit zunehmender Partikelgröße zunahm [16]. Aus diesen Ergebnissen lässt sich ableiten, dass insbesondere bei kleineren Partikeln die Haftkräfte gegenüber anderen Kräften, wie z. B. der Gewichtskraft, derart dominieren, dass kleine Partikel und ihr Freisetzungsverhalten nicht anhand einer Eigenschaft oder eines Parameters beschrieben werden kann.
4 Schlussfolgerungen und Ausblick
In der hier vorliegenden Arbeit wurde anhand von experimentellen Untersuchungen mit einem Rotationverfahren ein semiempirischer Kennwert abgeleitet. Anhand dieses Kennwerts wurden Prognosefunktionen (vgl. Regressionsfunktionen in Bild 4) entwickelt, die eine Abschätzung der Staubungsneigung ermöglichen. Die hier aufgezeigten Prognosefunktionen sind nur bei getrockneten Materialien anwendbar. Bedingt durch die Komplexität der Prozesse, die zu einer Staubfreisetzung führen können, ist es sehr schwierig, einen analytischen Ansatz mit einer quantitativen Aussage in Bezug auf einzelne Partikelgrößenfraktionen zu finden. Trotzdem konnten durch die hier beschriebenen Experimente verteilungs- und materialspezifische Parameter identifiziert werden, die einen signifikanten Einfluss auf die Staubungsneigung eines Materials zeigten. Anhand der hier entwickelten Prognosefunktionen ist es möglich, für die Beanspruchung von Schüttgütern durch Rutsch- und Fallbewegungen in einem Rotationsverfahren, die zu erwartende Staubungsneigung eines Materials auf der Basis von verteilungs- und materialspezifischen Parametern abzuschätzen.
Danksagung
Der Deutschen Forschungsgemeinschaft (DFG) wird für die Förderung des Projektes „Eigenschaftsfunktion zur Berechnung der Staubungsneigung von Pulvern“ (SCHM 810/36) im Rahmen des Schwerpunktprogrammes „Dynamische Simulation vernetzter Feststoffprozesse“ (SPP 1679) gedankt.
Literatur
- [1] Hughes, D.; Ogden, T. L. (Hrsg.): Dustiness estimation methods for dry materials. British Occupational Hygiene Society technical guide No. 4. Leeds: H and H Scientific Consultants, 1985.
- [2] Hamelmann, F.; Schmidt, E.: Messverfahren zur Bestimmung des Staubungsvermögens von dispersen Pulvern. Chem.-Ing.-Tech. 74 (2002) Nr. 12, S. 1666-1676.
- [3] Hamelmann, F.; Schmidt, E.: Methoden zur Charakterisierung des Staubungsverhaltens von Pulvern. Chem.-Ing.-Tech. 75 (2003) Nr. 6, S. 696-700.
- [4] Schmidt, E.: Fraktionsfreisetzungsgrad – Ein neuer Ansatz zur Quantifizierung der Staubungsneigung von Pulvern. Chem.-Ing.-Tech. 87 (2015) Nr. 5, S. 638-643.
- [5] Sicherheitsdatenblatt Arizona Staub. Hrsg.: Fa. KSL Staubtechnik (2014).
- [6] Sicherheitsdatenblatt Baustellenschmutz. Hrsg.: Fa. KSL Staubtechnik (2014).
- [7] Sicherheitsdatenblatt ECE R-45. Hrsg.: Fa. KSL Staubtechnik (2014).
- [8] Sicherheitsdatenblatt KSL 11047. Hrsg.: Fa. KSL Staubtechnik (2014).
- [9] Technisches Datenblatt Pural NF. Hrsg. Fa. Sasol (2014).
- [10] Technisches Datenblatt Ulmer Weiss XMF. Hrsg.: Fa. Eduard Merkle (2014).
- [11] Schmidt, E.: Kurz gefasste Grundlagen der Partikelcharakterisierung und der Partikelabscheidung. Aachen: Shaker 2001.
- [12] Stiess, M.: Mechanische Verfahrenstechnik. Berlin: Springer 2009.
- [13] Sachs, L.: Angewandte Statistik: Anwendung statistischer Methoden. Berlin: Springer 2004.
- [14] Schwister, K. (Hrsg): Taschenbuch der Verfahrenstechnik. Fachbuchverlag Leipzig im Carl-Hanser-Verlag, 2010.
- [15] DIN 55992-1 Bestimmung einer Maßzahl für die Staubentwicklung von Pigmenten und Füllstoffen – Teil 1: Rotationsverfahren. Berlin: Beuth 2006.
- [16] Lopez-Lilao, A.; Bruzi, M.; Sanfelix, V.; Gozalbo, A.; Mallol, G.; Monfort, E.: Evaluation of the Dustiness of Different Kaloin Samples. J. Occup. Environ. Hyg. 12 (2015) Nr. 8, S. 547-554.
- [17] Schmidt, E.; Müller, O.: Strömungskräfte auf Partikeln in Gasen. Düsseldorf: VDI 1997.
- [18] Davidson, P. A.: Turbulence: an introduction for scientists and engineers. Oxford University Press, 2004.
- [19] Schubert, H. (Hrsg.): Handbuch der mechanischen Verfahrenstechnik. Bd. 1: Partikeleigenschaften, Mikroprozesse, Makroprozesse, Zerteilen, Agglomerieren, Trennen, Mischen, Schüttgut. Weinheim: Wiley-VCH 2003.
Dr.-Ing. Tim Londershausen, Prof. Dr.-Ing. habil. Eberhard Schmidt, Bergische Universität Wuppertal, Institut für Partikeltechnologie, Wuppertal.