Stabilitäts- und Zuverlässigkeitsanalyse von Kreiszylinderschalen unter Axialdruck bezogen auf zufällige geometrische Imperfektionen – Teil 2: Stochastische Modellierung der geometrischen Imperfektionen, stochastische Simulation und Zuverlässigkeitsanalyse
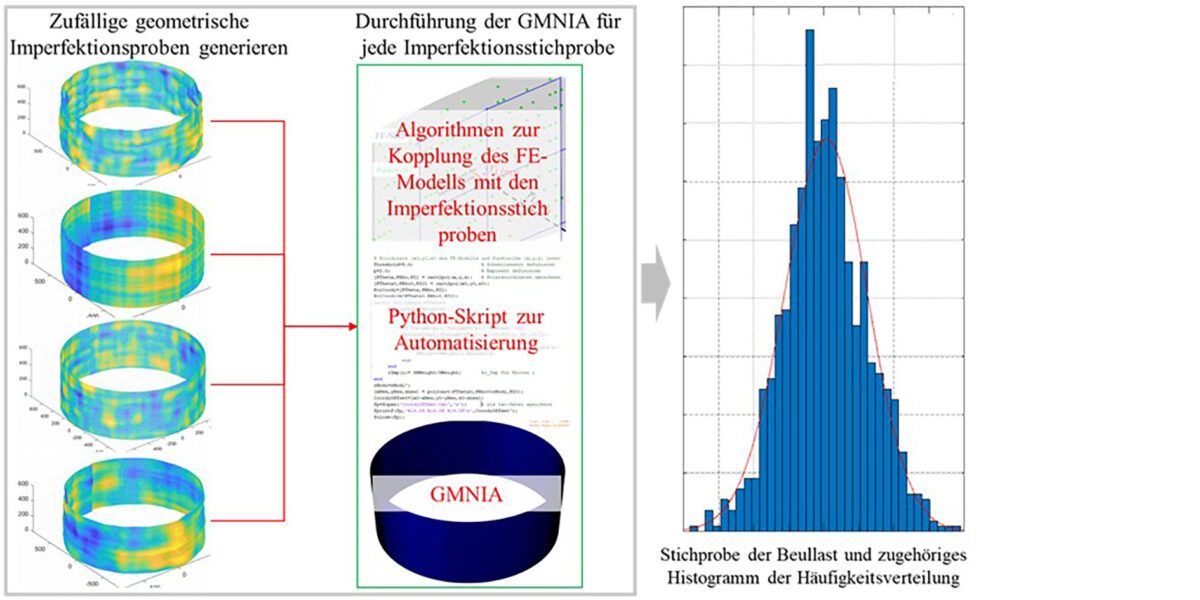
Schematischer Ablauf der probabilistischen Beullastanalyse kreiszylindrischer Schalen. Grafik: Z. Li
Z. Li, H. Pasternak
Bauingenieur Jahrgang 100 (2025) Heft 10
Publikationsdatum: 01.10.2025
doi.org/10.37544/0005-6650-2025-10-51
Zusammenfassung Aufbauend auf den im Teil 1 dargestellten experimentellen Untersuchungen und numerischen Analysen wird im Teil 2 ein probabilistischer Ansatz zur Beschreibung und Bewertung der Beultragfähigkeit von kreiszylindrischen Schalen unter axialer Druckbeanspruchung vorgestellt. Die zufälligen geometrischen Imperfektionen werden mithilfe der zweidimensionalen Zufallsfeldtheorie erfasst, durch eine Fourier-Reihenentwicklung beschrieben und stochastisch parametrisiert. Basierend auf zufällig generierten geometrischen Imperfektionen wird ein nicht-invasives stochastisches Finite-Elemente-Methode (SFEM) eingesetzt, um deren Einfluss auf die Beultragfähigkeit systematisch zu analysieren. Die numerischen Berechnungen erfolgen mit einem kommerziellen FE-Programm unter Anwendung der geometrisch und materiell nichtlinearen Analyse in Kombination mit einer begleitenden Eigenwertanalyse. Die nichtlineare Berechnung ermöglicht die Identifizierung der maßgebenden Beulformen und zugehörigen Versagenslasten. Die resultierenden Beullasten werden statistisch ausgewertet und mithilfe des Maximum-Entropie-Ansatzes an optimale Wahrscheinlichkeitsverteilungen angepasst. Auf Grundlage dieser Verteilungen wird eine Zuverlässigkeitsanalyse durchgeführt, in der exemplarisch der Einfluss unterschiedlicher Lastverteilungen und Sicherheitsanforderungen untersucht wird. Die Ergebnisse zeigen, dass die Traglastverteilung der Kreiszylinderschalen maßgeblich von der räumlichen Ausprägung und den statistischen Eigenschaften der geometrischen Imperfektionen beeinflusst wird. Die eingesetzte stochastische Analyse ermöglicht eine realitätsnahe und robuste Quantifizierung von Unsicherheiten in der Stabilitätsanalyse dünnwandiger Schalentragwerke und bildet die Grundlage für zukünftige zuverlässigkeitsbasierte Bemessungskonzepte.
Structural Stability and Reliability of Cylindrical Shells under Axial Compression considering Random Geometric Imperfections – Part 2: Stochastic Modelling of Geometric Imperfections, Stochastic Simulation and Reliability Analysis
Abstract Building upon the experimental investigations and numerical analyses presented in Part 1, Part 2 introduces a probabilistic approach to characterize and evaluate the buckling strength of cylindrical shells under axial compression. Random geometric imperfections are captured using the theory of two-dimensional random fields and represented by a Fourier series expansion that is stochastically parameterised. Based on randomly generated geometric imperfections, a non-intrusive stochastic FEM is employed to systematically analyze their influence on the buckling capacity. Numerical simulations are performed using a commercial finite element program, applying a geometrically and materially nonlinear analysis in combination with an accompanying eigenvalue analysis. The resulting buckling loads are statistically evaluated and fitted to suitable probability distributions using the maximum entropy method. Based on these distributions, a reliability analysis is performed to evaluate the influence of different load distributions and safety measures. The results demonstrate that the distribution of buckling strength in cylindrical shells is significantly impacted by the spatial structure and statistical properties of the geometric imperfections. This methodology provides a robust and realistic quantification of uncertainties in the stability analysis of thin-walled shell structures, offering a basis for future reliability-based design concepts.